10 лет назад прошёл самый долгий Гран При в истории!
День 12 июня 2011 года надолго запомнился и тем, кто в тот день вышел на старт Гран При Канады, и всем командам Формулы 1, и болельщикам. Но, возможно, больше всего он запомнился гоночным журналистам, ведь тот рабочий день (точнее, ночь с переходом в утро!) был рекордным по продолжительности – потому что именно тогда состоялась самая долгая гонка в истории чемпионата.
Виной всему были обстоятельства непреодолимой силы, и тут поневоле вспоминается классическое «У природы нет плохой погоды».
Накануне той гонки на монреальском автодроме имени Жиля Вильнёва прогноз пророчил дождь. Поэтому в McLaren настроили машины на несколько большую прижимную силу, и это оказалось правильным решением, хотя отчасти из-за него Льюис Хэмилтон и Дженсон Баттон показали только 5-й и 7-й результаты в квалификации.
Днём в воскресенье действительно лил настолько сильный дождь, что старт был дан за автомобилем безопасности. Первые четыре круга пелотон ездил за ним, затем началась борьба на трассе, но понятно, что асфальт был залит водой, и машины сильно скользили.
Хэмилтон попытался атаковать Марка Уэббера, ехавшего 4-м, но между машинами произошёл контакт, в результате чего оба потеряли позиции. Льюис откатился на 6-ю, а гонщик Red Bull Racing – вообще на 14-ю.
К 6-му кругу Хэмилтон догнал Баттона, но тот допустил ошибку в последней шикане, и молодой напарник на выходе из поворота попытался его опередить. Их машины практически поравнялись, однако Дженсон продолжал ехать по своей обычной траектории, поскольку не видел Льюиса – столкновение было неизбежным, и этот круг, а с ним и гонка для чемпиона мира 2008 года закончились ударом об отбойник.
Выехал автомобиль безопасности, а после рестарта Баттон получил штрафной проезд по пит-лейн за превышение скорости в ситуации, когда был введён режим сейфти-кара.
На 20-м круге дождь хлынул снова, в очередной раз появился автомобиль безопасности, и вскоре стало понятно, что в таких условиях гонку продолжать невозможно, на трассе было слишком много воды. Перерыв продолжался более двух часов, а когда наконец-то был дан рестарт, выяснилось, что уже пора переходить на промежуточную резину.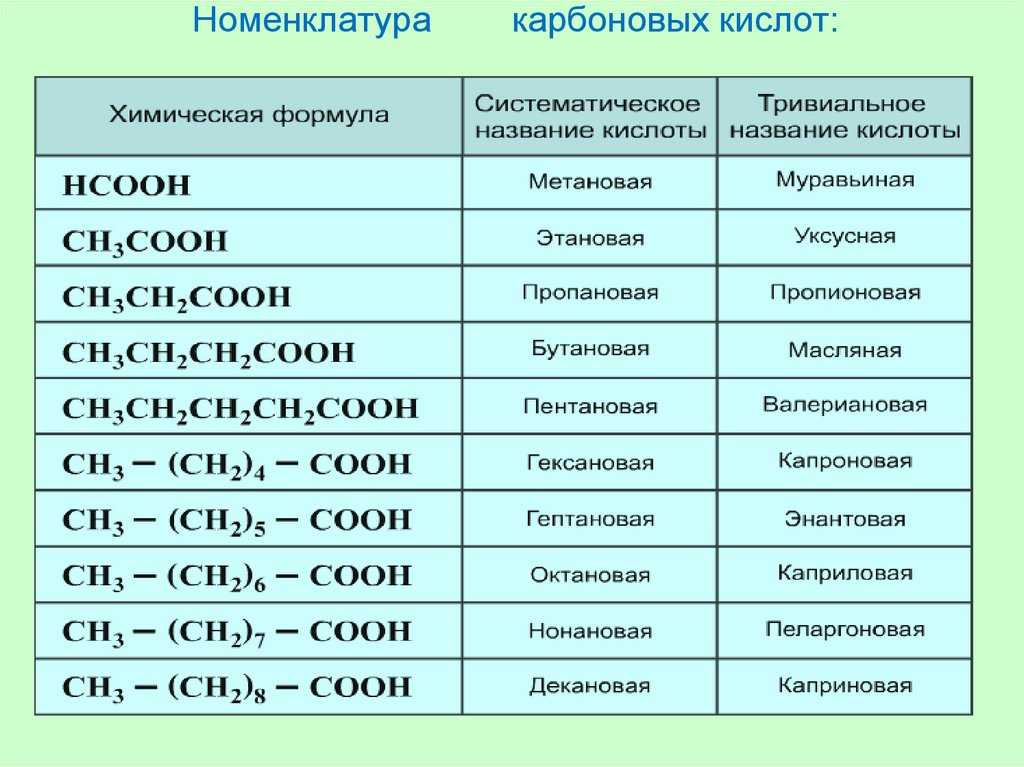 Все поехали в боксы, но после своих пит-стопов Ferrari Фернандо Алонсо и McLaren Баттона вернулись на трассу почти одновременно.
Все поехали в боксы, но после своих пит-стопов Ferrari Фернандо Алонсо и McLaren Баттона вернулись на трассу почти одновременно.
Началась короткая дуэль, между машинами произошёл контакт, после чего Ferrari застряла на поребрике, и автомобиль безопасности выехал снова. А вот Дженсону пришлось возвращаться в боксы из-за проколотого колеса.
Финал гонки получился фантастически захватывающим. Баттону удалось догнать и опередить сначала Марка Уэббера, затем Михаэля Шумахера – во многом благодаря тому, что McLaren британца была настроена на более сильный прижим и лучше держала трассу.
Дженсон ехал уже вторым и ринулся в погоню за лидировавшим Себастьяном Феттелем, начал его прессинговать и вынудил ошибиться в 7-м повороте. В итоге Баттон одержал победу – и это после двух инцидентов и шести пит-стопов! По ходу рекордно длинной гонки, продолжавшейся 4 часа 4 минуты и 39,537 секунды, он успел побывать на всех позициях, от последней до первой, и, наверное, это была лучшая победа в его карьере.
Некоторые считают, что тот Гран При вообще стал самой интересной гонкой в новейшей истории Формулы 1. Но однозначно, что она была самой продолжительной! Именно после неё были скорректированы правила и введён лимит по времени: теперь Гран При не может продолжаться дольше двух часов.
gran-turismo.com
по состоянию на 18 декабря 2019 г.
WeatherTech Raceway Laguna Seca
- Общая длина : 3 602 м
- Общий перепад высот : 55 м
- Повороты : 11
- Самая длинная прямая : 453 м
Автодром WeatherTech Raceway Laguna Seca расположен в самом сердце знаменитой “Кремниевой долины” — в 100 км к югу от города Сан-Хосе в северной Калифорнии. Его техничная трасса, состоящая преимущественно из медленных и средних поворотов, со всех сторон окружена пустыней. Песок, задуваемый ветром на дорожное покрытие, ухудшает сцепление с трассой, поэтому гонщикам приходится особенно тщательно контролировать скорость. Любая ошибка здесь может закончиться аварией.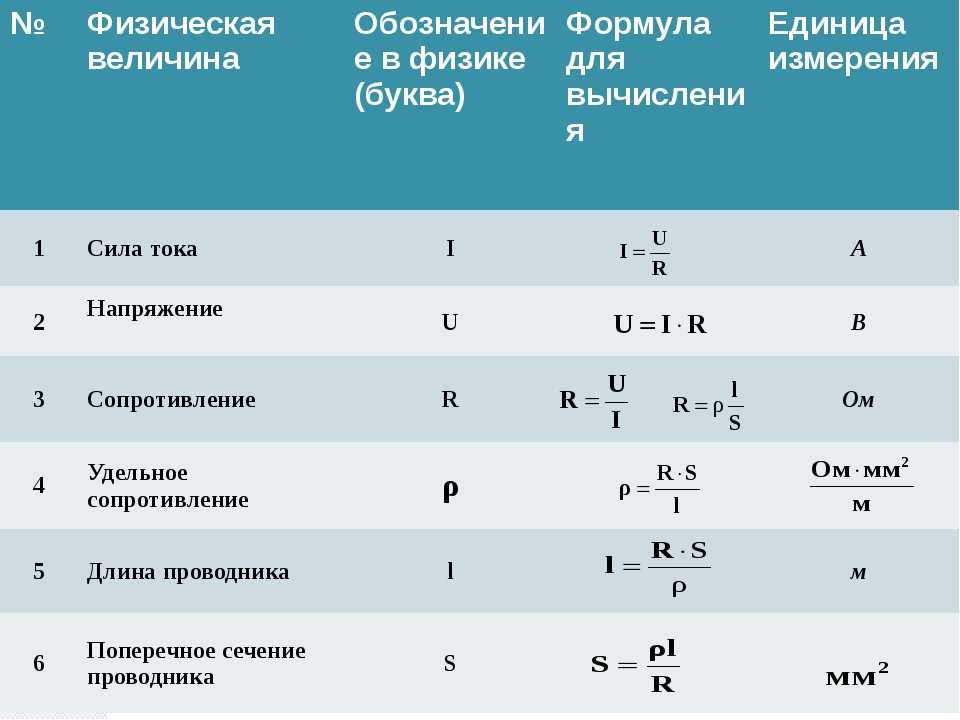 Вдобавок, трасса обладает непростым рельефом: одной из ее знаменитых особенностей является 15-метровый нисходящий поворот “Штопор”. Таких впечатлений, как на Laguna Seca, вы не получите больше нигде в мире.
Вдобавок, трасса обладает непростым рельефом: одной из ее знаменитых особенностей является 15-метровый нисходящий поворот “Штопор”. Таких впечатлений, как на Laguna Seca, вы не получите больше нигде в мире.
Circuit de Spa-Francorchamps
- Общая длина : 7 004 м
- Общий перепад высот : 104 м
- Повороты : 21
- Самая длинная прямая : 751,84 м
Трасса Spa-Francorchamps расположена в 40 км юго-восточнее Льежа — индустриального города в восточной Бельгии. На этой скоростной и техничной трассе длиной более 7 км, проложенной в гористой местности с большими перепадами высот, проводятся самые разные соревнования — от этапов “Формулы-1” до гонок на выносливость. Ее знаменитые повороты, в число которых входит расположенный на подъеме “О Руж”, сверхбыстрый левый “Бланшимон” и шикана “Автобусная остановка”, видели немало легендарных битв. Многие гонщики считают “Спа” одной из самых сложных трасс в мире.
- Дождливая погода
Goodwood Motor Circuit
- Общая длина : 3 809 м
- Общий перепад высот : 10 м
- Повороты : 7
- Самая длинная прямая : 514 м
Историческая трасса Goodwood Motor Circuit, расположенная в пригороде Чичестера на юге Англии, помнит многих знаменитых гонщиков. Проложенная вокруг аэропорта “Чичестер-Гудвуд”, она, в отличие от большинства современных автодромов, окружена безмятежными сельскими пейзажами. Трасса, включающая в себя ряд средних и быстрых поворотов, в целом является довольно скоростной, что в сочетании со сложным рельефом делает заезды поистине незабываемыми.
AUTOPOLIS INTERNATIONAL RACING COURSE
- Общая длина : 4 674 м
- Общий перепад высот : 52 м
- Повороты : 18
- Самая длинная прямая : 902 м
Знаменитый автодром AUTOPOLIS расположен посреди горной гряды в префектуре Оита острова Кюсю на юго-западе Японии. Его трасса достаточно сложна и технична: если сектор 1 представляет собой простой скоростной участок, то в секторах 2 и 3 гонщика ждут связки поворотов самых разных конфигураций. Ситуацию осложняют и многочисленные перепады высот, на которых максимальный подъем составляет 7,2%, а максимальный спуск — 10%. Чтобы пройти круг на этой трассе, не совершив ни одной ошибки, требуется серьезная концентрация. Помимо основного варианта, используемого для международных гонок, трасса доступна и в коротком варианте, где поворот 10 становится последним.
Его трасса достаточно сложна и технична: если сектор 1 представляет собой простой скоростной участок, то в секторах 2 и 3 гонщика ждут связки поворотов самых разных конфигураций. Ситуацию осложняют и многочисленные перепады высот, на которых максимальный подъем составляет 7,2%, а максимальный спуск — 10%. Чтобы пройти круг на этой трассе, не совершив ни одной ошибки, требуется серьезная концентрация. Помимо основного варианта, используемого для международных гонок, трасса доступна и в коротком варианте, где поворот 10 становится последним.
- 2 варианта
Circuit de Barcelona-Catalunya — Grand Prix
- Общая длина : 4 655 м
- Общий перепад высот : 30 м
- Повороты : 16
- Самая длинная прямая : 1047 м
Автодром Circuit de Barcelona-Catalunya, находящийся в 30 км от испанского города Барселона, был открыт в сентябре 1991 года к Олимпийским играм. С тех пор на нем проводится Гран-при Испании в классе “Формула-1” и другие соревнования мирового уровня.
- 1 вариант
Fuji Speedway
- Общая длина : 4 563 м
- Общий перепад высот : 40 м
- Повороты : 16
- Самая длинная прямая : 1475 м
Этот знаменитый японский автодром расположен у подножия великой горы Фудзи. Открывшийся в 1961 году, он принял немало крупных соревнований и видел бессчетное множество эпических поединков между гонщиками. Первая половина его трассы, расположенная за знаменитой 1,5-км прямой, представляет собой скоростной участок со средними и быстрыми поворотами, а вторая расположена на уклоне и является более техничной. Поскольку характеристики этих двух участков заметно различаются, большую роль на этой трассе играет регулировка машины.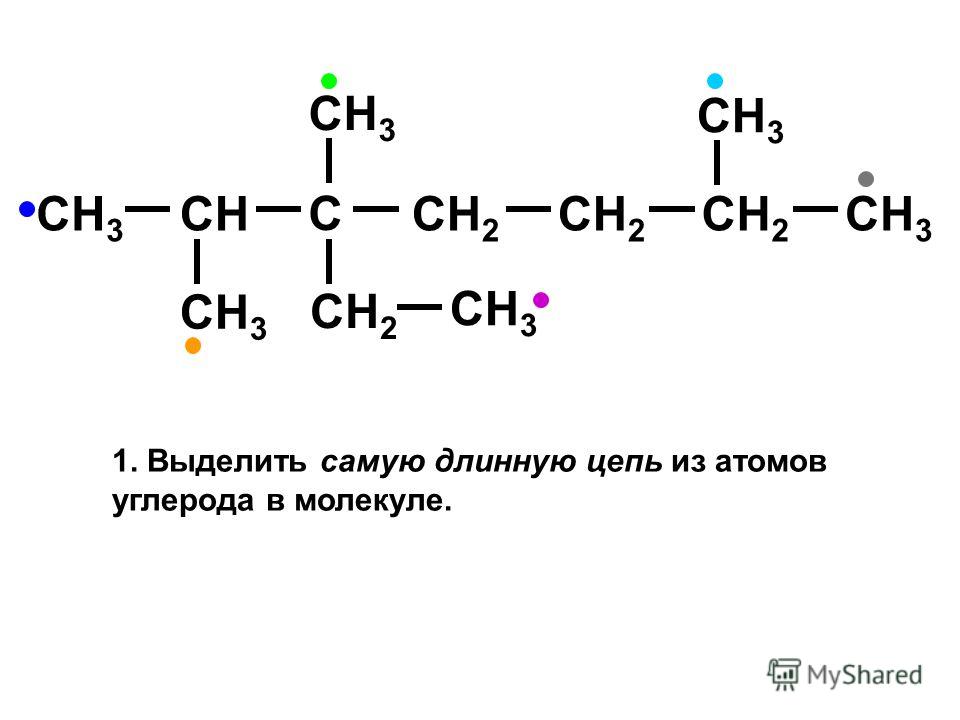
- 2 варианта
Red Bull Ring
- Общая длина : 4 318 м
- Общий перепад высот : 65,45 м
- Повороты : 10
- Самая длинная прямая : 939 м
Эта трасса расположена среди зеленых холмов к северо-западу от старинного австрийского города Грац. Впервые открытая в 1969 г. под названием “Остеррайхринг”, с 1997 по 2010 г. она была известна как “А1 Ринг”. В ее составе есть как медленные крутые повороты, так и быстрые скоростные участки; в целом, эта трасса достаточно скоростная. При этом она сложнее, чем кажется на первый взгляд: хотя ее планировка выглядит простой, холмистая местность, по которой она проложена, создает значительные перепады высот. Время круга здесь в большой степени зависит от мастерства гонщика. Трасса доступна как в полном, так и в укороченном варианте.
- 2 варианта
- Дождливая погода
Circuit de la Sarthe
- Общая длина : 13 629 м
- Общий перепад высот : 37,3 м
- Повороты : 38
- Самая длинная прямая : 1 679 м
Эта трасса расположена в городе Ле-Ман на западе Франции. Она известна в первую очередь как место проведения “24 часов Ле-Мана” — одной из 3 величайших гонок мира. Открывшаяся в 1923 г., эта трасса за свою долгую историю повидала множество знаменитых поединков. Будучи одной из самых высоко расположенных в мире, она предъявляет особые требования к аэродинамике гоночных машин. Помимо современного варианта с шиканой и общей дистанцией 13,6 км, мы предлагаем вам старый вариант этой трассы с 5,7-километровой прямой, идеально подходящей для проверки аэродинамических характеристик.
- 2 варианта
Tsukuba Circuit
- Общая длина : 2 045 м
- Общий перепад высот : 5,3 м
- Повороты : 8
- Самая длинная прямая : 445 м
Этот популярный автодром, расположенный в городе Симоцума (префектура Ибараки), является ближайшим к японской столице Токио.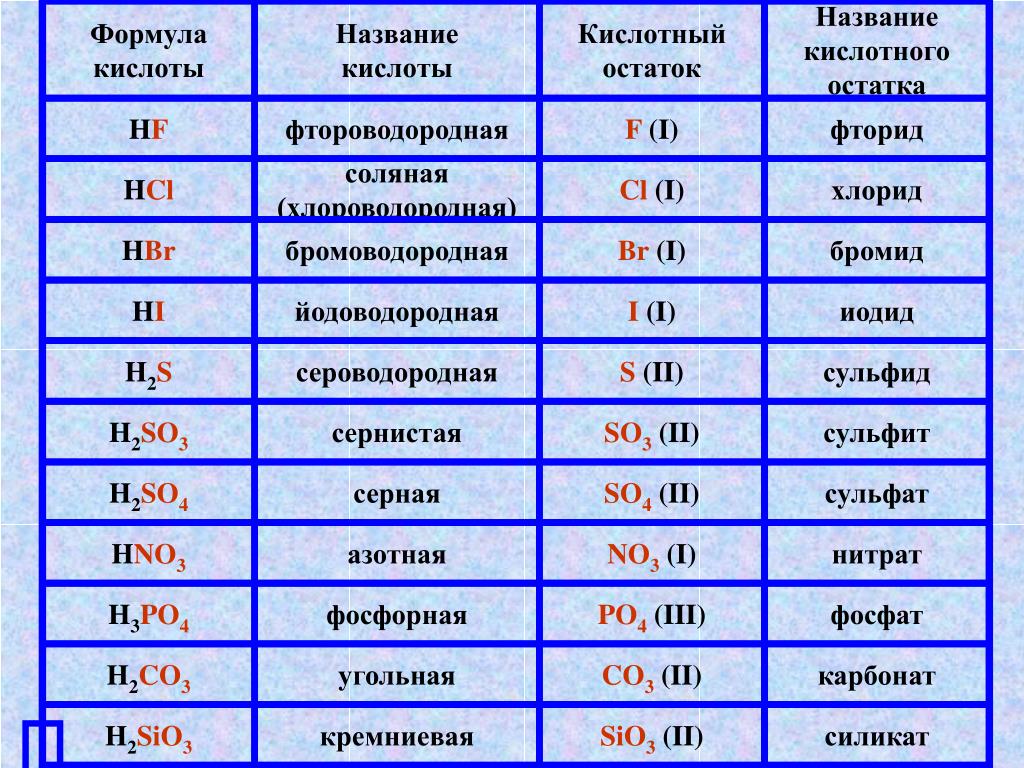 Длина его трассы составляет всего 2045 м, однако на этой короткой дистанции собрано достаточно много разных поворотов. Гонщики любят эту трассу именно за техничность. Открывшийся в 1970 г. автодром принимает множество крупных соревнований, в том числе японские кузовные чемпионаты, а также регулярно используется автомобильной прессой для проведения тестовых заездов.
Длина его трассы составляет всего 2045 м, однако на этой короткой дистанции собрано достаточно много разных поворотов. Гонщики любят эту трассу именно за техничность. Открывшийся в 1970 г. автодром принимает множество крупных соревнований, в том числе японские кузовные чемпионаты, а также регулярно используется автомобильной прессой для проведения тестовых заездов.
Autodromo Nazionale Monza
- Вариант с шиканой : Общая длина : 5 793 м
- Общий перепад высот : 13,5 м
- Повороты : 11
- Самая длинная прямая : 938 м
Этот знаменитый автодром расположен в живописном национальном парке “Монца” на окраине Милана в северной Италии. Построенный в 1922 году, он является третьим среди старейших автодромов мира после “Бруклендса” и “Индианаполиса”. Изначально его трасса включала в себя профилированный овал, а сейчас она представляет собой сочетание шикан и сопряженных поворотов, соединенных длинными прямыми. Вашему вниманию предлагается два варианта этой скоростной и динамичной трассы: с шиканой и без.
Вашему вниманию предлагается два варианта этой скоростной и динамичной трассы: с шиканой и без.
- 2 варианта
Autódromo De Interlagos
- Общая длина : 4 309 м
- Общий перепад высот : 44 м
- Повороты : 15
- Самая длинная прямая : 589 м
“Интерлагос”, любимый автодром легендарного гонщика Айртона Сенны, расположен в бразильском городе Сан-Паулу. Он примечателен нетипичным для “Формулы-1” направлением круга против часовой стрелки, а также сочетанием длинных поворотов с большими перегрузками и медленного техничного участка. Его трасса, требующая стабильности на скоростных участках и маневренности в крутых поворотах, представляет особую сложность для гонщиков. С другой стороны, рост вашего мастерства на ней будет особенно заметно влиять на время круга.
Nürburgring
- Вариант для 24-часовых гонок : Общая длина : 25 378 м
- Общий перепад высот : 300 м
- Повороты : 89
- Самая длинная прямая : 2 135 м
Эта трасса признана одной из самых сложных в мире.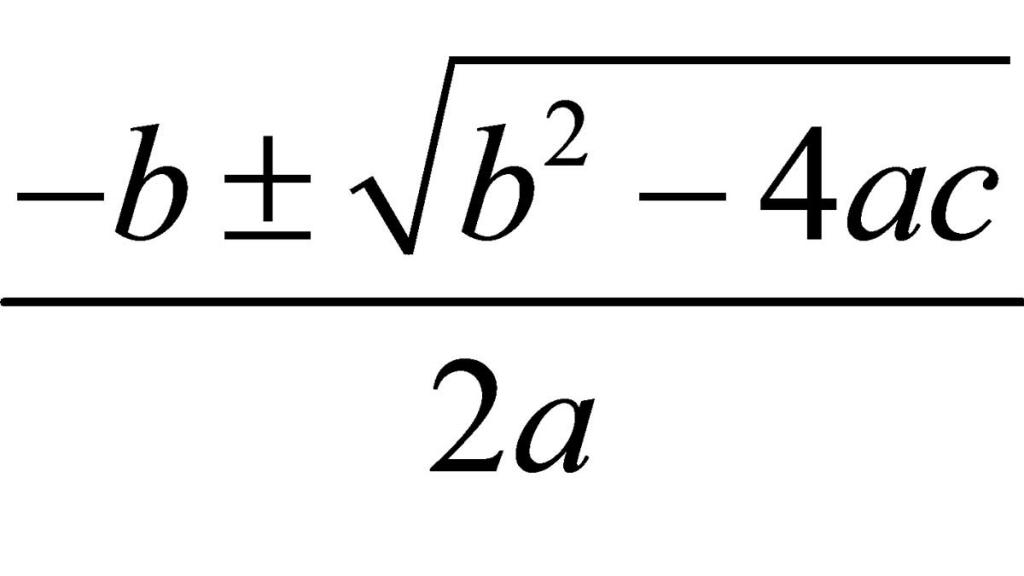 Ее длина превышает 20 км, а перепад высот достигает 300 м. Чтобы запомнить и научиться использовать все тонкости и нюансы ее рельефа, требуется довольно много времени. Трасса доступна в двух вариантах: легендарном “Нордшляйфе”, на котором прошло немало исторических гонок, и более современном, используемом для “24 часов Нюрбургринга”. Помимо дневных условий, позволяющих любоваться красотами окрестных лесов, для нее доступны и ночные.
Ее длина превышает 20 км, а перепад высот достигает 300 м. Чтобы запомнить и научиться использовать все тонкости и нюансы ее рельефа, требуется довольно много времени. Трасса доступна в двух вариантах: легендарном “Нордшляйфе”, на котором прошло немало исторических гонок, и более современном, используемом для “24 часов Нюрбургринга”. Помимо дневных условий, позволяющих любоваться красотами окрестных лесов, для нее доступны и ночные.
- 3 варианта
Willow Springs International Raceway
- Big Willow : Общая длина : 3 951 м
- Общий перепад высот : 50 м
- Повороты : 10
- Самая длинная прямая : 756 м
Этот знаменитый американский автодром существует уже более 60 лет. В прошлом он принимал легендарную серию CART, а сейчас является популярным центром любительских гонок. Помимо основного варианта Big Willow, он доступен в более техничном варианте Streets of Big Willow Springs и укороченном Horse Thief Mile.
- 5 вариантов
Brands Hatch
- Grand Prix : Общая длина : 3 946 м
- Общий перепад высот : 35 м
- Повороты : 9
- Самая длинная прямая : 475 м
В прошлом этот автодром, расположенный в английском графстве Кент, принимал этапы “Формулы-1”, а сейчас на нем проводятся кузовные гонки и британские чемпионаты “Формулы-3”. Его трасса, проложенная в живописном лесу, примечательна крутыми подъемами и спусками, однако благодаря относительно простой планировке доступна не только опытным гонщикам, но и новичкам. Вдобавок к полному варианту Grand Prix, мы включили в игру ее вариант Indy с укороченным средним участком.
- 2 варианта
Mount Panorama Motor Racing Circuit
- Общая длина : 6 213 м
- Общий перепад высот : 174 м
- Повороты : 23
- Самая длинная прямая : 1 916 м
На этом важнейшем автодроме Австралии проводятся такие крупные соревнования, как “12 часов Батерста”. Его первый и последний участки состоят из длинных скоростных прямых, а вот средний участок, расположенный на холме, представляет собой техничную серию закрытых поворотов со значительными перепадами рельефа. Этот разительный контраст составляет главную изюминку Mount Panorama. Не пожалейте времени на освоение этой непростой трассы.
Его первый и последний участки состоят из длинных скоростных прямых, а вот средний участок, расположенный на холме, представляет собой техничную серию закрытых поворотов со значительными перепадами рельефа. Этот разительный контраст составляет главную изюминку Mount Panorama. Не пожалейте времени на освоение этой непростой трассы.
Suzuka Circuit
- Общая длина : 5 807 м
- Общий перепад высот : 40 м
- Повороты : 20
- Самая длинная прямая : 1 200 м
Эта знаменитая трасса, помнящая немало легендарных гонок, была построена еще до того, как в Японии появились автомагистрали. Она обладает крайне необычной планировкой в форме восьмерки с пересечением по виадуку. Лучшие гонщики из разных стран мира восхищаются ее многочисленными уникальными поворотами. Вдобавок к полному варианту, длина которого составляет 5,8 км, мы предлагаем укороченный восточный вариант, включающий в себя первую половину трассы.
- 2 варианта
Sardegna — дорожная
- Общая длина : 5 113 м
- Общий перепад высот : 38 м
- Повороты : 15
- Самая длинная прямая : 915 м
Новая дорожная трасса создана по мотивам итальянского курортного острова Сардиния, омываемого водами Средиземного моря. Проложенная по перекрытым участкам дорог общего пользования, она включает в себя как длинные скоростные прямые, так и сложные техничные повороты. На второй половине дистанции ее рельеф усложняется, а ширина уменьшается, что делает обгоны еще более рискованными. Помимо самого длинного варианта A, она доступна в варианте B (3 893 м) и C (2 661 м).
- 6 вариантов
Special Stage Route X
- Общая длина : 30,283 м
- Общий перепад высот : 65 м
- Повороты : 2
- Самая длинная прямая : 12 000 м
Знаменитый 30-километровый овал Special Stage Route X, на котором проводились экзамены и скоростные гонки в прошлых версиях Gran Turismo, снова вернулся в игру. Его конфигурация предельно проста: две 12-километровые прямые, соединенные двумя профилированными поворотами. Эта трасса идеально подходит для испытаний максимальной скорости и гонок с активным использованием “воздушного мешка”.
Его конфигурация предельно проста: две 12-километровые прямые, соединенные двумя профилированными поворотами. Эта трасса идеально подходит для испытаний максимальной скорости и гонок с активным использованием “воздушного мешка”.
- 1 вариант
Sainte-Croix Circuit
- Sainte-Croix Circuit A : Общая длина : 9 477 м
- Общий перепад высот : 44 м
- Повороты : 19
- Самая длинная прямая : 915 м
Вымышленная трасса по мотивам окрестностей реально существующего озера Сен-Круа, расположенного в регионе Прованс на юге Франции. Ее длинный 10-километровый маршрут изобилует развилками и доступен в трех вариантах, обозначенных буквами A, B и C. На трассе имеются как 90-градусные, так и дугообразные повороты. Для каждого варианта предусмотрена возможность прохождения в обоих направлениях.
- 6 вариантов
Kyoto Driving Park
- Yamagiwa : Общая длина : 4 912 м
- Общий перепад высот : 38,6 м
- Повороты : 15
- Самая длинная прямая : 743 м
Этот автодром расположен в горах на окраине древнего города Киото, который в прошлом был столицей Японии. Он доступен в трех вариантах: полном дорожном Yamagiwa, любительском Miyabi и объединяющем их Yamagiwa + Miyabi. В его оформлении используются традиционные японские мотивы: вы увидите деревянные постройки в зоне пит-лейна, характерные орнаменты по обочинам, каменное покрытие трассы и бамбуковые ограждения.
Он доступен в трех вариантах: полном дорожном Yamagiwa, любительском Miyabi и объединяющем их Yamagiwa + Miyabi. В его оформлении используются традиционные японские мотивы: вы увидите деревянные постройки в зоне пит-лейна, характерные орнаменты по обочинам, каменное покрытие трассы и бамбуковые ограждения.
- 5 вариантов
Tokyo Expressway
- Центр внешнего кольца : Общая длина : 7 301 м
- Общий перепад высот : 32 м
- Повороты : 13
- Самая длинная прямая : 2 000 м
Эта трасса создана по мотивам токийской скоростной магистрали Metropolitan Expressway, которая вьется среди небоскребов, построенных в период японского экономического бума. Ее варианты “Центр внешнего кольца” и “Центр внутреннего кольца” проложены по центральным районам, а в вариантах “Восток внешнего кольца” и “Восток внутреннего кольца” вам предстоит проехать более 7 км по ночному городу. Еще два варианта основаны на реально существующей токийской магистрали “Сюто”: вариант “Юг внешнего кольца” включает в себя множество разнообразных поворотов, среди которых есть “шпильки” и шиканы, а “Юг внутреннего кольца” проходит через контейнерный терминал.
- 6 вариантов
- Дождливая погода
Dragon Trail
- Берег : Общая длина : 5 209 м
- Общий перепад высот : 38 м
- Повороты : 18
- Самая длинная прямая : 653 м
Эта дорожная трасса, расположенная в хорватском регионе Далмация, проходит по берегам лазурной Адриатики среди горных склонов. Она имеет треугольную планировку с тремя крутыми поворотами и сложным рельефом, на котором есть подъемы, спуски и ровный участок вдоль побережья. На трассе воссоздана уникальная природа Далмации со скалистыми берегами, на которых растут оливы, сосны и пальмы.
- 4 варианта
Autodromo Lago Maggiore
- Общая длина : 5 809 м
- Общий перепад высот : 74 м
- Повороты : 17
- Самая длинная прямая : 800 м
Эта техничная трасса расположена на берегу озера Маджоре в северной Италии среди живописных Альп. Ее длина составляет около 5,8 км, на которых собрано множество уникальных поворотов, подъемов и спусков. К примеру, перепад высот на главной прямой достигает 40 метров, а сразу после нее расположена “шпилька” с креном 20 градусов. Таких уникальных впечатлений вы не получите больше нигде. Помимо основного, трасса доступна в трех укороченных вариантах: центральном, восточном и западном.
Ее длина составляет около 5,8 км, на которых собрано множество уникальных поворотов, подъемов и спусков. К примеру, перепад высот на главной прямой достигает 40 метров, а сразу после нее расположена “шпилька” с креном 20 градусов. Таких уникальных впечатлений вы не получите больше нигде. Помимо основного, трасса доступна в трех укороченных вариантах: центральном, восточном и западном.
- 8 вариантов
Northern Isle Speedway
- Общая длина : 900 м
- Общий перепад высот : 0 м
- Повороты : 4
- Самая длинная прямая : 134 м
Этот короткий овал длиной полмили (около 900 м) весьма популярен в американском автоспорте. Большой угол крена, достигающий 31 градуса, в сочетании с шириной 16 м позволяет ехать по нему двум и даже трем машинам в ряд. Примечательной особенностью трассы является массивная трибуна для зрителей, под которой располагаются современные боксы. Овал доступен не только в дневном варианте, но и в ночном с красивой подсветкой.
Blue Moon Bay Speedway
- Общая длина : 3 200 м
- Общий перепад высот : 0 м
- Повороты : 3
- Самая длинная прямая : 1 060 м
Этот современный автодром расположен на американском побережье среди пальм. Рядом с ним имеется курортный отель и аэропорт. Его овальная трасса длиной около 2 миль включает в себя три поворота, соединенных тремя прямыми. Все повороты обладают разными радиусами и профилями, что существенно разнообразит выбор тактики. Помимо основной трассы, на автодроме доступны два варианта с техничными участками во внутренней части овала.
- 6 вариантов
Broad Bean Raceway
- Общая длина : 1 665 м
- Общий перепад высот : 0 м
- Повороты : 5
- Самая длинная прямая : 386 м
Эта овальная трасса находится на территории огромного спорткомплекса в Японии. Ее планировка представляет собой классический эллипс, но с дополнительным поворотом на прямой, благодаря чему трасса похожа на бобовое зерно. По сравнению со стандартным овалом, она дает заметно больше возможностей для обгона при торможении.
Ее планировка представляет собой классический эллипс, но с дополнительным поворотом на прямой, благодаря чему трасса похожа на бобовое зерно. По сравнению со стандартным овалом, она дает заметно больше возможностей для обгона при торможении.
- 2 варианта
Alsace
- Деревня : Общая длина : 5 423 м
- Общий перепад высот : 57,3 м
- Повороты : 15
- Самая длинная прямая : 450 м
Французский регион Эльзас известен своей богатой историей. Эта трасса длиной 5,4 км проходит вокруг небольшого эльзасского городка на реке Рейн, частично захватывая дороги общего пользования. Она включает в себя преимущественно средние и быстрые повороты, но из-за многочисленных перепадов высот богата живописными видами. Очарования ей добавляет и густая зелень с красивыми цветами на обочинах.
- 2 варианта
Fishermans Ranch
- Общая длина : 6 893 м
- Общий перепад высот : 145 м
- Повороты : 40
- Самая длинная прямая : 434 м
Эта грунтовая трасса, вьющаяся среди кактусов и кустарников, расположена в засушливом регионе США к югу от Скалистых гор. Ее длина составляет 7 км, на которых имеется множество разнообразных поворотов, крутых подъемов и спусков, а также больших трамплинов. Чтобы удержать машину на грунте, вам потребуется одновременно работать газом и тормозом.
Ее длина составляет 7 км, на которых имеется множество разнообразных поворотов, крутых подъемов и спусков, а также больших трамплинов. Чтобы удержать машину на грунте, вам потребуется одновременно работать газом и тормозом.
- 2 варианта
Sardegna
- Мельницы : Общая длина : 3 310 м
- Общий перепад высот : 75 м
- Повороты : 12
- Самая длинная прямая : 298 м
Эта скоростная грунтовая трасса расположена на итальянском острове Сардиния, омываемом водами Средиземного моря. Она примечательна ветряками, возвышающимися на обочинах, а также рощами олив и пиний. Учтите, что после первого скоростного участка, расположенного на спуске, трасса начинает идти в гору.
- 2 варианта
Colorado Springs
- Озеро : Общая длина : 2 990 м
- Общий перепад высот : 15 м
- Повороты : 18
- Самая длинная прямая : 177 м
Город Колорадо-Спрингс, расположенный в американском штате Колорадо, известен как место проведения гонки “Пайкс-Пик”. В нем имеется большое озеро, по берегам которого и проложена эта грунтовая трасса длиной около 3 км. Ее рельеф по большей части плоский, однако в нескольких местах возможны прыжки, способные заметно повлиять на исход гонки. Гонки по грунту среди живописных хвойных и широколиственных деревьев доставят вам огромное удовольствие!
В нем имеется большое озеро, по берегам которого и проложена эта грунтовая трасса длиной около 3 км. Ее рельеф по большей части плоский, однако в нескольких местах возможны прыжки, способные заметно повлиять на исход гонки. Гонки по грунту среди живописных хвойных и широколиственных деревьев доставят вам огромное удовольствие!
- 2 варианта
Вернуться к началу страницы
10 самых важных уравнений в истории
Какое самое длинное уравнение в мире?
По данным Sciencealert, самое длинное математическое уравнение содержит около 200 терабайт текста. Названная проблемой булевых пифагорейских троек, она была впервые предложена математиком из Калифорнии Рональдом Грэмом еще в 1980-х годах.
Почему уравнения важны?
Уравнения используются каждый день для многих, многих вещей. Они помогают вам искать в Интернете, заставлять ваш компьютер работать и поддерживать самолеты в воздухе, и это лишь некоторые из них.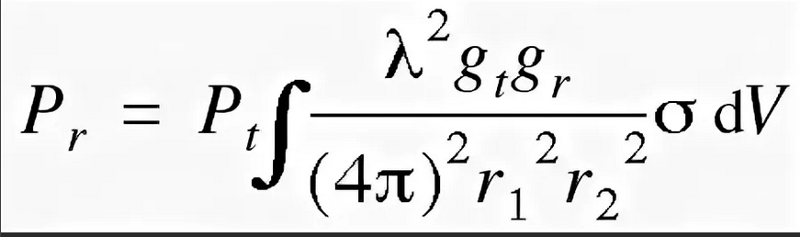
Что такое уравнение теории хаоса?
«Теория хаоса — это раздел математики, посвященный поведению динамических систем, которые очень чувствительны к начальным условиям. Теория хаоса — это междисциплинарная теория, утверждающая, что в пределах кажущейся случайности хаотических сложных систем существуют лежащие в основе закономерности, постоянные петли обратной связи. , повторение, самоподобие, фракталы и самоорганизация». — Википедия.
Уравнение выглядит следующим образом:-
Изменено с news.bitofnews.comЭта теория эффективно помогает нам иметь дело со сложными системами, поведение которых очень чувствительно к небольшим изменениям условий, поэтому небольшие изменения могут привести к непредвиденным последствиям.
Теория хаоса — это наука о сюрпризах, и не всегда приятных сюрпризах.
10 уравнений, которые изменили мир
Вот десять самых важных уравнений, изменивших мир. Этот список далеко не исчерпывающий и не имеет определенного порядка.
1. Теорема Пифагора
Источник: MaxpixelЭто уравнение, являющееся основным элементом школьных уроков математики, фактически изменило мир. Это позволило нам составить более совершенные карты и помочь найти кратчайшее расстояние между объектами; среди других вещей.
Он также широко используется в архитектуре, деревообработке и многих других областях.
2. Исчисление
«Исчисление, первоначально называвшееся исчислением бесконечно малых или «исчислением бесконечно малых», представляет собой математическое исследование непрерывного изменения, точно так же, как геометрия — это изучение формы, а алгебра — изучение обобщения арифметических операций». — Википедия.
Он был независимо разработан великим Исааком Ньютоном и сэром Готфридом Лейбницем.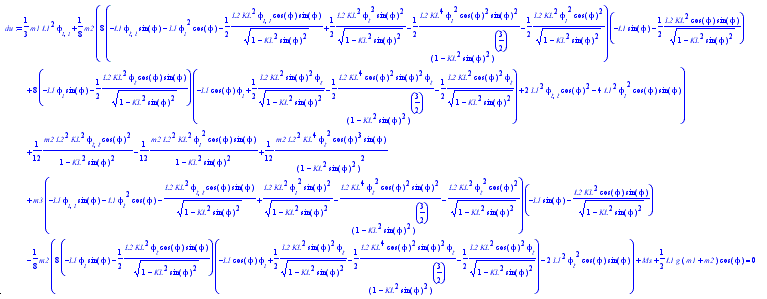 После своего изобретения он объединил алгебру и геометрию как один из столпов математики.
После своего изобретения он объединил алгебру и геометрию как один из столпов математики.
3. Логарифмы
Логарифмы — это еще один тип уравнений, которые изменили мир. Они помогали нам производить утомительные расчеты до того, как появились калькуляторы.
Самый популярный
Логарифм — это величина, представляющая степень, в которую нужно возвести фиксированное число (основание), чтобы получить данное число. Использование таблиц логарифмов позволило исключить многие утомительные этапы вычислений в таких областях, как геодезия, навигация и инженерия.
4. Теория относительности
Источник: Peat Bakke/FlickrЗнаменитые уравнения теории относительности Эйнштейна не только ответили на многие ранее нерешенные вопросы, но и помогли изменить наш взгляд на время, пространство и гравитацию.
Он используется, чтобы помочь объяснить все, от черных дыр до большого взрыва, ядерной энергии, а также GPS на наших телефонах.
5. Нормальное распределение
Сегодня мы все знакомы с кривыми нормального распределения. Они помогают описать распределение данных в данном наборе.
Его можно использовать для чего угодно: от IQ среди населения до результатов экзамена среди группы студентов. При нормальном распределении большинство точек данных попадают где-то посередине, и меньшее количество людей ближе к крайним точкам.
6. Уравнение Шредингера
Источник: YassineMrabet/ Wikimedia CommonsУравнение Шредингера необходимо для современных компьютерных чипов и лазеров. По-видимому, это также помогает держать кошек в состоянии анабиоза между жизнью и смертью.
А если серьезно, это уравнение буквально навсегда изменило область квантовой физики. Это линейное уравнение в частных производных, описывающее волновую функцию квантово-механической системы. Его открытие стало важной вехой в развитии квантовой механики.
Его открытие стало важной вехой в развитии квантовой механики.
7. Закон всемирного тяготения Ньютона
«Закон всемирного тяготения Ньютона утверждает, что каждая частица притягивает любую другую частицу во Вселенной с силой, которая прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояние между их центрами». — Википедия.
Закон всемирного тяготения Ньютона — одно из самых фундаментальных уравнений в физике.
8. Волновое уравнение
«Волновое уравнение описывает поведение волн — вибрацию гитарной струны, рябь в пруду после брошенного камня или свет, исходящий от лампы накаливания. Волновое уравнение было ранним дифференциальным уравнением. , а методы, разработанные для решения уравнения, открыли дверь для понимания и других дифференциальных уравнений». — Businessinsider.com.
Он является важным компонентом электромагнетизма, оптики, гидродинамики и теплопередачи.
9. Второй закон термодинамики
«Здесь утверждается, что в закрытой системе энтропия (S) всегда постоянна или возрастает. Термодинамическая энтропия, грубо говоря, является мерой того, насколько система неупорядочена. который начинается в упорядоченном, неравномерном состоянии — скажем, горячая область рядом с холодной областью — всегда будет иметь тенденцию к выравниванию, когда тепло будет течь от горячей области к холодной, пока не будет равномерно распределено». — Businessinsider.com.
Помогает нам, среди прочего, понять направление теплопередачи. Эту теорию можно выразить через изменение энтропии системы (dS). В этом уравнении dS рассчитывается путем измерения количества тепла, поступившего в замкнутую систему (δQ), деленного на общую температуру (T) в точке, где происходил перенос тепла.
10. Преобразование Фурье
Это уравнение лежит в основе современной обработки сигналов. Это также важно для анализа сигналов и сжатия данных.
Это также важно для анализа сигналов и сжатия данных.
«Преобразование Фурье необходимо для понимания более сложных волновых структур, таких как человеческая речь. Учитывая сложную, беспорядочную волновую функцию, такую как запись разговора человека, преобразование Фурье позволяет нам разбить беспорядочную функцию на комбинацию числа простых волн, что значительно упрощает анализ». — Businessinsider.com.
Для вас
наука
Поскольку ксенотрансплантация предположительно считается универсальным решением проблемы нехватки донорских органов, исследователи говорят нам, что есть нечто большее, чем то, что соответствует гену.
Дина Тереза | 16.08.2022
Наука Поведение темной материи может противоречить нашей лучшей теории Вселенной
Пол Ратнер| 27.07.2022
культураВечеринка в честь Хэллоуина: 3 рецепта пьянящих коктейлей, которые пробудят в вас внутреннего инженера
Стивен Вичинанца| 31. 10.2022
10.2022
Еще новости
наука
Впервые исследователи обнаружили редкий минерал, который происходит непосредственно из нижней мантии Земли
Сад Агард| 28.11.2022
новшество
Можно ли дышать на Марсе? Европа обитаема? Что работа НАСА говорит о будущем человечества
Дина Тереза | 17.08.2022
здоровье
Первый в мире скрининг-тест на рак поджелудочной железы показывает, как черви вынюхивают опухоли
Лукия Пападопулос| 04.12.2022
В: Какое самое сложное уравнение?
Физик : Если у вас достаточно места на доске и вам абсолютно нечего делать, вы можете записывать числа, буквы (по-гречески, если вы δυσάρεστος) и математические операторы, и в итоге у вас будет самое длинное уравнение, которое когда-либо было написано. вниз. Так что, если вы действительно хотите увидеть самое сложное уравнение, запишитесь на несколько недель по болезни. Лучше задать вопрос: «Какое уравнение самое (но не излишне) сложное?».
Лучше задать вопрос: «Какое уравнение самое (но не излишне) сложное?».
Существует множество бесконечно длинных уравнений, но зачастую они достаточно просты, чтобы их можно было записать компактно. Например, это уравнение можно продолжать вечно, но оно довольно прямолинейно: в каждом члене вы переворачиваете знак и увеличиваете знаменатель от одного нечетного числа к другому. Вы можете написать это на математическом языке как . Как и само число π, эта сумма бесконечна, но она несложна. Вы можете описать это просто и так, что любой (при наличии достаточного времени и мела) сможет найти столько цифр числа π, сколько захочет. Это основная идея «Колмогоровской сложности»; длина кратчайшего из возможных наборов письменных инструкций, которые могут привести к заданному результату (неважно, сколько времени потребуется для фактического его вычисления).
Если вы ищете уравнение, которое нужно усложнить, вам стоит поискать физику (я имею в виду, для чего еще вам нужна математика?). Если вы хотите описать поведение мяча, летящего по воздуху, недостаточно сказать «он поднимается, а затем опускается»; для точного расчета траектории падающих объектов требуется минимальное количество математики, и все гораздо сложнее.
Если вы хотите описать поведение мяча, летящего по воздуху, недостаточно сказать «он поднимается, а затем опускается»; для точного расчета траектории падающих объектов требуется минимальное количество математики, и все гораздо сложнее.
Возможно, вселенная довольно сложна. Но, как и π, это обманчиво (мы надеемся). Если вы хотите сделать что-то вроде, скажем, описания гравитационных взаимодействий каждой звезды в галактике, вы бы сделали это, пронумеровав звезды (не торопитесь: звезда 1, звезда 2, …, звезда n), определите положение и массу каждой, и , а затем найти силу, действующую на каждую звезду, создаваемую всеми остальными. На практике это абсурд (в Млечном Пути несколько сотен миллиардов звезд, но мы не можем видеть большинство из них, потому что на пути есть галактика), но уравнение, которое вы использовали бы, довольно простое. Сила, действующая на звезду k, равна: . Это всего лишь закон всемирного тяготения Ньютона, повторенный для каждой возможной пары звезд и суммированный. Таким образом, хотя сама ситуация сложна, уравнение, ее описывающее, — нет. Очевидно, что если вам нужно уравнение, которое действительно должно быть сложным, вам не нужна сложная ситуация, вам нужна сложная динамика.
Таким образом, хотя сама ситуация сложна, уравнение, ее описывающее, — нет. Очевидно, что если вам нужно уравнение, которое действительно должно быть сложным, вам не нужна сложная ситуация, вам нужна сложная динамика.
Уравнение притяжения между многими объектами — это просто уравнение притяжения между каждой парой сложенных объектов. Не намного сложнее.
Весь смысл физики, помимо понимания вещей, состоит в том, чтобы как можно проще описать законы Вселенной. С этой целью физики любят говорить о «лагранжианах». Получив лагранжиан системы, вы можете описать поведение этой системы, применив «принцип наименьшего действия», согласно которому поведение системы (орбита, по которой движется планета, путь света через материалы и т. д.) всегда будет таким, что «выбранный» путь будет иметь минимальный суммарный лагранжиан на этом пути. Это милый рецепт для краткого и одновременного описания большого количества динамики, которым Колмогоров мог бы гордиться.
Лагранжиан дает каждой точке на этой картинке значение, а сумма по всему пути есть «действие».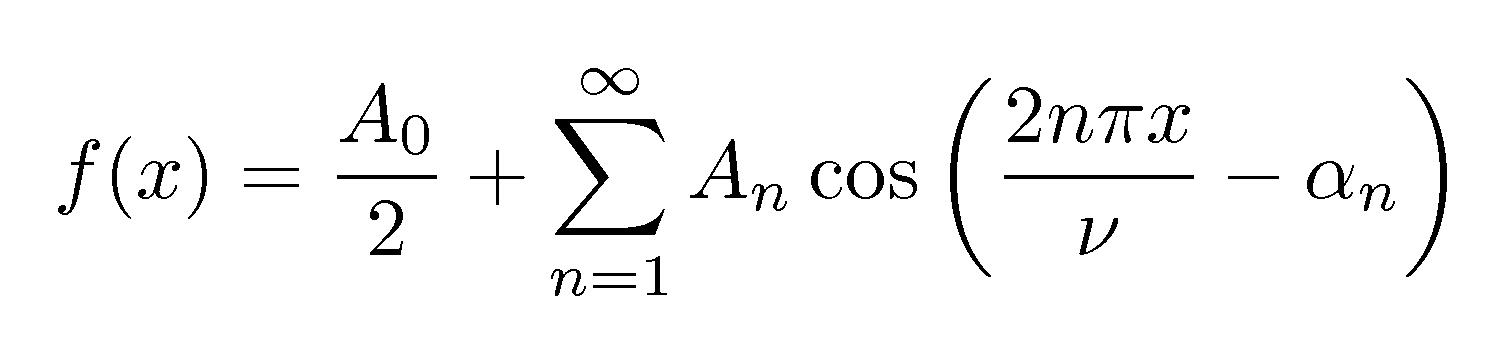 Принцип наименьшего действия гласит, что путь, по которому фактически пойдет система, предполагает наименьшее действие. С этим принципом один лагранжиан может быть использован для вывода многих физических законов одновременно, так что это хороший кандидат для уравнений, которые не являются излишне сложными .
Принцип наименьшего действия гласит, что путь, по которому фактически пойдет система, предполагает наименьшее действие. С этим принципом один лагранжиан может быть использован для вывода многих физических законов одновременно, так что это хороший кандидат для уравнений, которые не являются излишне сложными .
Например, вы можете почти мгновенно суммировать ньютоновскую физику. Вместо того, чтобы говорить о кинетической энергии, импульсе и падении, вы можете просто сказать: «Чуваки и чуваки, если позволите, лагранжиан для объекта, летящего по воздуху вблизи поверхности Земли, равен , где m — масса, v — скорость, z — высота». Из этого single формула, вы получаете сохранение энергии, сохранение количества движения (при движении боком), а также ускорение за счет силы тяжести. Существуют также лагранжианы для всего, от обращения планет до электромагнитных полей.
Обычно, когда вы снова и снова смотрите на одну и ту же динамику, используемые уравнения не становятся намного сложнее (хотя их решения определенно усложняются).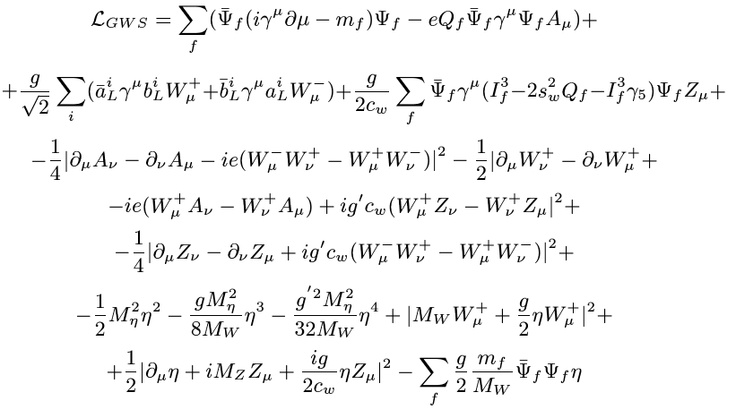 И если вы хотите описать динамику системы, лагранжианы — чрезвычайно компактный способ сделать это. Так какое же самое (но не излишне) сложное уравнение во Вселенной? Возможно, это лагранжиан Стандартной модели, который охватывает динамику всех видов частиц и все их взаимодействия. Примечательно, что это не распространяется на гравитацию, но будьте круты. Это незавершенная работа.
И если вы хотите описать динамику системы, лагранжианы — чрезвычайно компактный способ сделать это. Так какое же самое (но не излишне) сложное уравнение во Вселенной? Возможно, это лагранжиан Стандартной модели, который охватывает динамику всех видов частиц и все их взаимодействия. Примечательно, что это не распространяется на гравитацию, но будьте круты. Это незавершенная работа.
Уравнение всего (кроме гравитации).
В некотором смысле это уравнение представляет собой сжатые данные. Вся соответствующая динамика присутствует, но нужно многое распаковать, прежде чем это станет отдаленно очевидным. Все уравнения должны иметь некоторый контекст, прежде чем они будут что-то делать или даже что-то означать. Вот почему учебники по математике в основном состоят из слов. «2+2=4» ничего не значит для пришельца, пока вы не объясните ему, что означает каждый из этих символов и как они используются. В случае лагранжиана Стандартной модели каждый из этих символов много значит, в самом уравнении используются симпатичные краткие приемы, и оно даже не описывает динамику без привязки к принципу наименьшего действия. Но, учитывая все это, он описывает самую сложную вещь, которую мы можем описать, то есть почти все, без излишней многословности («математики»?) об этом.
Но, учитывая все это, он описывает самую сложную вещь, которую мы можем описать, то есть почти все, без излишней многословности («математики»?) об этом.
Ответ Gravy : Это не часть вопроса, но если вы изучали физику, вы, вероятно, видели уравнения кинетической энергии, импульса и ускорения в однородном гравитационном поле (например, вы испытываете прямо сейчас). Но если вы на самом деле не физик, вы, вероятно, никогда не сходили с ума, увидев работу Лагранжа. Эта подливка полна исчисления и вводной физики.
«Действие», , является функцией пути, по которому движется система, . Точнее, это интеграл от лагранжиана между любыми двумя данными моментами времени:
, где t 1 и t 2 – время начала и окончания, – путь, – производная по времени (скорость) этого пути, – некоторая заданная функция от и . Если вы хотите выбрать путь, который экстремизирует (минимизирует или максимизирует) S, то вы можете сделать это, решив уравнения Эйлера-Лагранжа:
Это называется уравнениями Эйлера-Лагранжа (во множественном числе), потому что на самом деле это несколько уравнений. Каждая отдельная переменная (x 1 = x, x 2 =y, x 3 =z) говорит вам о другом. В обычном старом исчислении, если вы хотите найти значение x, которое экстремумирует функцию f(x), вы решаете значение x. Использование уравнений Эйлера-Лагранжа с философской точки зрения аналогично: чтобы найти путь, экстремальный S, вы решаете путь .
Каждая отдельная переменная (x 1 = x, x 2 =y, x 3 =z) говорит вам о другом. В обычном старом исчислении, если вы хотите найти значение x, которое экстремумирует функцию f(x), вы решаете значение x. Использование уравнений Эйлера-Лагранжа с философской точки зрения аналогично: чтобы найти путь, экстремальный S, вы решаете путь .
Лагранжиан из более раннего для свободно падающего объекта вблизи поверхности Земли: такая же ставка». Делая то же самое для x или y, вы получаете , что говорит о том, что «вещи не ускоряются вбок». И то, и другое полезно знать.
Хотите быть еще хитрее, обратите внимание, что этот лагранжиан не зависит от времени. Что означает, что . Следовательно, применяя цепное правило:
Но у нас есть уравнения Э-Л! Подставляем те:
И, следовательно:
Эта вещь в скобках постоянна (поскольку она никогда не меняется во времени). В случае мы находим, что эта константа равна:
Проницательные студенты-физики 1 узнают сумму кинетической энергии и гравитационного потенциала.
