Формула самая длинная – Ответы Mail.ru: Наверняка трассы Формулы-1 различаются по своей длине, отсюда вопрос: какая трасса Ф-1 из всех существовавших(щих) — triksklad.ru

Содержание

Майтотоксин — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 июня 2018; проверки требуют 10 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 июня 2018; проверки требуют 10 правок.

Майтотоксин — токсин небелковой природы, продуцируемый динофлагеллятами вида Gambierdiscus toxicus. Является одним из самых токсичных веществ, обнаруженных в живой природе, и, одновременно, одним из самых сложных по структуре веществ природного происхождения.

Майтотоксин чрезвычайно токсичен (доза в 130 нг/кг массы тела, при внутрибрюшинном введении, летальна для мышей)^[1] и обладает, вероятно, самым сложным строением из всех известных небелковых веществ природного происхождения (правильность установления структуры и пространственного строения молекулы майтотоксина и в настоящее время вызывает сомнения, а попытки осуществить его полный синтез, начатые ещё в середине 90-ых годов XX века, до сих пор не увенчались успехом).

Изначально майтотоксин был выделен из рыб вида Ctenochaetus striatus (полосатый хирург), обитающих в экосистемах коралловых рифов и питающихся планктоном (биоаккумуляция токсина в организме некоторых видов хищных рыб (барракуды, морской окунь, мурены, сибас и др.), питающихся полосатым хирургом, приводит к отравлению людей, употребляющих рыбу этих видов в пищу). На Таити этот вид рыб известен как «maito», что и дало название этому токсину^[2]^[3].

Структура и пространственное строение молекулы майтотоксина были установлены к середине 90-ых годов XX века с использованием новейших методов аналитической химии (масс-спектрометрия и двумерная спектроскопия ЯМР с предварительной частичной окислительной деградацией молекулы данного токсина). Но сомнения относительно правильности установления пространственного строения майтотоксина остаются до сих пор

[4].

Необычность и сложность структуры (в т.ч. наличие в молекулах множества хиральных центров) таких соединений как майтотоксин, палитоксин и др. делают установление их строения само по себе очень сложной задачей и требуют привлечения усилий как наиболее компетентных учёных, так и использования самых передовых методов химического и физико-химического анализа (в т.ч. таких, которые ранее просто не существовали)^[4]. Особую сложность представляет установление стереохимии (пространственного строения) подобных соединений. Даже само по себе получение достаточных количеств таких веществ является непростой задачей. Единственный доступный источник получения — выделение из живых организмов, которые осуществляют биосинтез либо биоаккумулируют их в себе (причём, как правило, содержание их очень невелико). К примеру, для получения в чистом виде майтотоксина пришлось на протяжении года культивировать динофлагеллят вида

Gambierdiscus toxicus для получения около 4000 литров культуры (с концентрацией клеток 2*10⁶/л), а затем применить многостадийный процесс выделения, концентрирования и очистки этого соединения. В итоге удалось получить порядка 5 мг(!) химически чистого майтотоксина^[4].

Работы над осуществлением полного синтеза майтотоксина были начаты ещё в 1996 г. и продолжаются (с перерывами) по настоящее время под руководством Кирьякоса Николау. Возглавляемые им группы учёных пока что смогли осуществить синтез некоторых отдельных частей, из которых состоит молекула майтотоксина^[5]^[6]^[7]^[8]^[2].

Молекула майтотоксина состоит из 32 конденсированных колец, содержит 28 гидроксильных и 22 метильные группы, а также 2 эфира серной кислоты. Кроме того, в ней есть 98 хиральных центров. Всё это делает задачу по выполнению полного химического синтеза майтотоксина исключительно сложной.

50 — 50 нг/кг массы тела (для мышей), что делает майтотоксин наиболее токсичным из всех известных веществ небелковой природы.

Физиологическое действие майтотоксина состоит в нарушении гомеостаза внутриклеточного содержания Ca²⁺. Резкое повышение содержания ионов Са²⁺ внутри клеток, в конечном счёте, приводит к их гибели. Точный молекулярный механизм действия майтотоксина неизвестен, но предполагается, что он связывается с Ca-АТФазой, превращая её в ионный канал, через который ионы Ca²⁺ начинают неконтролируемо поступать во внутриклеточное пространство^[9]^[10]^[11]^[12]

↑ Akihiro Yokoyama, Michio Murata, Yasukatsu Oshima, Takashi Iwashita, Takeshi Yasumoto. Some Chemical Properties of Maitotoxin, a Putative Calcium Channel Agonist Isolated from a MarineDinoflagellate (англ.) // The Journal of Biochemistry. — 1988-08-01. — Vol. 104, iss. 2. — P. 184–187. — ISSN 0021-924X. — DOI:10.1093/oxfordjournals.jbchem.a122438.

↑ ¹ ² Katrina Krämer2018-03-09T14:28:00+00:00. Maitotoxin (англ.). Chemistry World. Дата обращения 7 декабря 2019.
↑ Ю.А. Владимиров. Биоорганическая химия. — Москва: Просвещение, 1987. — С. 772. — 815 с.
↑ ¹ ² ³ В.А. Стоник, И.В. Стоник. Морские токсины: химические и биологические аспекты изучения (рус.) // Успехи химии : журнал. — 2010. — Т. 79, № 5. — С. 451-452.
↑ K. C. Nicolaou, Kevin P. Cole, Michael O. Frederick, Robert J. Aversa, Ross M. Denton. Chemical Synthesis of the GHIJK Ring System and Further Experimental Support for the Originally Assigned Structure of Maitotoxin // Angewandte Chemie International Edition. — 2007. — Т. 46, вып. 46. — С. 8875–8879. — ISSN 1521-3773. — DOI:10.1002/anie.200703742.
↑ K. C. Nicolaou, Michael O. Frederick, Antonio C. B. Burtoloso, Ross M. Denton, Fatima Rivas.
Chemical Synthesis of the GHIJKLMNO Ring System of Maitotoxin // Journal of the American Chemical Society. — 2008-06-01. — Т. 130, вып. 23. — С. 7466–7476. — ISSN 0002-7863. — DOI:10.1021/ja801139f.
↑ K. C. Nicolaou, Robert J. Aversa, Jian Jin, Fatima Rivas. Synthesis of the ABCDEFG Ring System of Maitotoxin // Journal of the American Chemical Society. — 2010-05-19. — Т. 132, вып. 19. — С. 6855–6861. — ISSN 0002-7863. — DOI:10.1021/ja102260q.
↑ K. C. Nicolaou, Philipp Heretsch, Tsuyoshi Nakamura, Anna Rudo, Michio Murata. Synthesis and Biological Evaluation of QRSTUVWXYZA′ Domains of Maitotoxin // Journal of the American Chemical Society. — 2014-11-19. — Т. 136, вып. 46. — С. 16444–16451. — ISSN 0002-7863. — DOI:10.1021/ja509829e.
↑ Yasushi Ohizumi, Takeshi Yasumoto. Contraction and increase in tissue calcium content induced by maitotoxin, the most potent known marine toxin, in intestinal smooth muscle (англ.) // British Journal of Pharmacology. — 1983. — Vol. 79, iss. 1. — P. 3–5. — ISSN 1476-5381. — DOI:10.1111/j.1476-5381.1983.tb10485.x.

↑ William G. Sinkins, Mark Estacion, Vikram Prasad, Monu Goel, Gary E. Shull. Maitotoxin converts the plasmalemmal Ca2+ pump into a Ca2+-permeable nonselective cation channel // American Journal of Physiology-Cell Physiology. — 2009-09-30. — Т. 297, вып. 6. — С. C1533–C1543. — ISSN 0363-6143. — DOI:10.1152/ajpcell.00252.2009.
↑ Mark Estacion, William P. Schilling. Maitotoxin-induced membrane blebbing and cell death in bovine aortic endothelial cells // BMC Physiology. — 2001-02-06. — Т. 1, вып. 1. — С. 2. — ISSN 1472-6793. — DOI:10.1186/1472-6793-1-2.
↑ Kevin K. W. Wang, Rathna Nath, Kadee J. Raser, Iradj Hajimohammadreza. Maitotoxin Induces Calpain Activation in SH-SY5Y Neuroblastoma Cells and Cerebrocortical Cultures // Archives of Biochemistry and Biophysics. — 1996-07-15. — Т. 331, вып. 2. — С. 208–214. — ISSN 0003-9861. — DOI:10.1006/abbi.1996.0300.

Самая красивая теорема математики: тождество Эйлера / Habr

Посмотрев лекцию профессора Робина Уилсона о тождестве Эйлера, я наконец смог понять, почему тождество Эйлера является самым красивым уравнением. Чтобы поделиться моим восхищением это темой и укрепить собственные знания, я изложу заметки, сделанные во время лекции. А здесь вы можете купить его прекрасную книгу.

Что может быть более загадочным, чем взаимодействие мнимых чисел с вещественными, в результате дающее ничто? Такой вопрос задал читатель журнала Physics World в 2004 году, чтобы подчеркнуть красоту уравнения Эйлера «e в степени i, умноженного на пи равно минус единице».

Рисунок 1.0: тождество Эйлера — e в степени i, умноженного на пи, плюс единица равно нулю.

Ещё раньше, в 1988 году, математик Дэвид Уэллс, писавший статьи для американского математического журнала The Mathematical Intelligencer, составил список из 24 теорем математики и провёл опрос, попросив читателей своей статьи выбрать самую красивую теорему. И после того, как с большим отрывом в нём выиграло уравнение Эйлера, оно получило званием «самого красивого уравнения в математике».

Рисунок 2.0: обложка журнала The Mathematical Intelligencer
Рисунок 3.0: опрос Дэвида Уэллса из журнала

Леонарда Эйлера называют самым продуктивным математиком за всю историю. Других выдающихся математиков вдохновляли его работы. Один из лучших физиков в мире, Ричард Фейнман, в своих знаменитых лекциях по физике назвал уравнение Эйлера «самой примечательной формулой в математике». Ещё один потрясающий математик, Майкл Атья, назвал эту формулу «…математическим аналогом фразы Гамлета — «быть или не быть» — очень короткой, очень сжатой, и в то же время очень глубокой».

Существует множество интересных фактов об уравнении Эйлера. Например, оно встречалось в некоторых эпизодах «Симпсонов».

Рисунок 4.0: в этой сцене уравнение Эйлера можно заметить на второй книге в самой правой стопке.
Рисунок 5.0: в этой сцене уравнение Эйлера написано на футболке второстепенного персонажа.

Также уравнение Эйлера стало ключевым пунктом в уголовном деле. В 2003 году аспирант Калифорнийского технологического института Билли Коттрелл писал краской на чужих спортивных автомобилях уравнение Эйлера. На суде он сказал: «Я знал теорему Эйлера с пяти лет, и её обязаны знать все«.

Рисунок 6.0: марка, выпущенная в 1983 году в Германии в память о двухсотлетии со смерти Эйлера.
Рисунок 7.0: марка, выпущенная Швейцарией в 1957 году в честь 250-й годовщины Эйлера.

Почему уравнение Эйлера так важно?

Вы имеете полное право задаться вопросом: почему Билли Коттрелл считал, что об уравнении Эйлера обязаны знать все? И был настолько в этом уверен, что начал писать его на чужих машинах? Ответ прост: Эйлер воспользовался тремя фундаментальными константами математики и применил математические операции умножения и возведения в степень, чтобы записать красивую формулу, дающую в результате ноль или минус один.

Константа e связана со степенными функциями.
Константа i является не вещественным, а мнимым числом, равным квадратному корню из минус единицы.
Знаменитая константа π (пи) связана с окружностями.

Впервые тождество Эйлера появилось в 1748 году в его книге Introductio in analysin infinitorum. Позже другие люди увидели, что эта формула связана с тригонометрическими функциями синуса и косинуса, и эта связь удивительна, ведь степенная функция стремится к бесконечности, а тригонометрические функции колеблются в интервале от — 1 до -1.

e в степени i, умноженного на ϕ (фи) = cos ϕ + i * sin ϕ

Рисунок 8.0: экспоненциальная функция y=e^x.
Рисунок 8.1: график тождества Эйлера.
Рисунок 8.2: частоты, испускаемые LC-цепью.

Показанные выше уравнения и графы могут показаться абстрактными, но они важны для квантовой физики и вычислений обработки изображений, и при этом зависят от тождества Эйлера.

1: число для счёта

Число 1 (единица) является основой нашей системы исчисления. С неё мы начинаем счёт. Но как мы считаем? Чтобы считать, мы используем цифры 0–9 и систему разрядов, определяющую значение цифры.

Например, число 323 означает 3 сотни, 2 десятка и 3 единицы. Здесь число 3 исполняет две разные роли, которые зависят от его расположения.

323 = (3*100) + (2*10) + (3*1)

Существует и другая система исчисления, называемая двоичной. В этой системе вместо 10 используется основание 2. Она широко применяется в компьютерах и программировании. Например, в двоичной системе:

1001 = (2³) + (0²) + (0¹) + (2⁰) = [9 в системе с основанием 10]

Кто создал системы исчисления? Как первые люди считали предметы или животных?

Как возникли наши системы исчисления? Как считали первые цивилизации? Мы точно знаем, что они не пользовались нашей разрядной системой. Например 4000 лет назад древние египтяне использовали систему исчисления с разными символами. Однако они комбинировали символы, создавая новый символ, обозначающий числа.

Рисунок 11: показанные здесь иероглифы образуют число 4622; это одно из чисел, вырезанных на стене в храме в Карнаке (Египет).
Рисунок 12: иероглифы — это изображения, обозначающие слова, а в данном случае — числа.

В то же время, но в другом месте ещё один социум обнаружил способ подсчёта, но в нём тоже использовались символы. Кроме того, основанием их системы исчисления было 60, а не 10. Мы используем их метод счёта для определения времени; поэтому в минуте 60 секунд, а в часе 60 минут.

Рисунок 13: вавилонские числа из шестидесятиричной системы счисления (с основанием 60).

Тысячу лет спустя древние римляне изобрели римские числа. Для обозначения чисел они использовали буквы. Римская нотация не считается разрядной системой, потому что для многих значений нашей системы счисления в ней использовались разные буквы. Именно по этой причине для счёта они использовали абакус.

Рисунок 14: романский абакус в шестнадцатеричной (с основанием 16) системе счисления
Рисунок 15: таблица преобразования из арабских в римские числа

Древние греки тоже не использовали разрядную систему счисления. Греческие математики обозначали числа буквами. У них были специальные буквы для чисел от 100 до 900. Многие люди в то время считали греческие числа запутанными.

Рисунок 15: таблица букв древних греков.

В то же самое время китайские математики начали использовать для расчётов небольшие бамбуковые палочки. Этот китайский способ счёта называют первой десятичной разрядной системой.

Рисунок 16: китайский способ счёта с числами-палочками. Использовался как минимум с 400 года до нашей эры. Квадратная счётная доска использовалась примерно до 1500 года, когда её заменил абакус.

Однако самая уникальная система счёта использовалась индейцами майя. Их система счисления имела основание 20. Для обозначения чисел от 1 до 19 они использовали точки и линии. Чем же отличалась их система счисления? Для каждого числа они использовали изображения голов и отдельный символ нуля 0.

Рисунок 17: Система счисления майя с основанием 20, в которой числа обозначались головами
Рисунок 18: ещё один способ записи чисел майя.

0: число для обозначения ничего

Некоторые цивилизации использовали пробелы, чтобы, например, отличать число 101 от 11. Спустя какое-то время начало появляться особое число — ноль. К примеру, в пещере в индийском городе Гвалиор археологи обнаружили на стене число 270, в котором был ноль. Самое первое зафиксированное использование нуля можно увидеть в Бодлианской библиотеке.
Рисунок 19: вырезанный на стене храма в Гвалиоре круг обозначает ноль. Ему примерно 1500 лет.
Рисунок 20: чёрные точки в манускрипте Бакхшали обозначают нули; это самый старый письменный пример использования числа, ему примерно 1800 лет.

Примерно 1400 лет назад были записаны правила вычислений с нулём. Например, при сложении отрицательного числа и нуля получается то же отрицательное число. Деление на нуль не допускается, потому что если разделить на ноль, то мы получим число, которое может быть равно любому нужному нам числу, что должно быть запрещено.

Вскоре после этого многими людьми были опубликованы книги по арифметике, распространяющие использование индо-арабской записи чисел. Ниже показана эволюция индо-арабских чисел. В большинстве стран используется индо-арабская система чисел, но арабские страны до сих пор пользуются арабскими числами.

Рисунок 21: на этой схеме показана эволюция чисел, происходящих от чисел брахми и заканчивающаяся числами, которыми мы используем и сегодня.
Рисунок 22: классическая гравюра «Арифметика» из Margarita Philosophica Грегора Рейша, на которой изображено соревнование между Боэцием, улыбающимся после открытия индо-арабских чисел и письменных вычислений, и нахмуренным Пифагором, до сих пор пытающимся пользоваться счётной доской.

Пи (π): самое известное иррациональное число

Пи — самое популярное из известных нам иррациональных чисел. Пи можно найти двумя способами: вычислив соотношение длины окружности к её диаметру, или соотношение площади круга к квадрату его радиуса. Евклид доказал, что эти соотношения постоянны для всех окружностей, даже для луны, пенни, шины и т.д.

π = окружность / диаметр ИЛИ π = площадь круга / радиус²

Рисунок 22: анимированная связь между окружностью и диаметром в отношении пи.

Так как иррациональные числа наподобие пи бесконечны и не имеют повторений, мы никогда не закончим записывать пи. Оно продолжается вечно. Есть люди, запомнившие множество десятичных разрядов пи (нынешний рекорд — 70 000 цифр! Источник: «Книга рекордов Гиннесса» ).

Рисунок 23: данные опроса 941 респондентов для определения процента людей, способных запомнить знаки пи после запятой.
Рисунок 24: На стене станции метро Karlsplatz в Вене записаны сотни разрядов пи.

На данный момент компьютеры смогли вычислить всего 2,7 триллиона разрядов пи. Может казаться, что это много, но на самом деле этот путь бесконечен.

Как я сказал выше, число пи нашёл Евклид. Но как поступали люди до Евклида, когда им нужно было найти площадь круга? Историки обнаружили вавилонскую глиняную табличку, в которой было записано отношение периметра шестиугольника к диаметру описанной вокруг него окружности. После вычислений полученное число оказалось равным 3.125. Это очень близко к пи.

Рисунок 24: вавилонская глиняная табличка с отношением периметра шестиугольника к длине описанной окружности.
Рисунок 25: Numberwarrior

Древние египтяне тоже близко подобрались к значению пи. Историки обнаружили документ, показывающий, как древние египтяне нашли число пи. Когда историки перевели документ, то нашли такую задачу:

Например, чтобы найти площадь поля диаметром 9 хета (1 хет = 52,35 метра), нужно выполнить следующее вычисление:
Вычесть 1/9 диаметра, а именно 1. Остаток равен 8. Умножить его на 8, что даёт нам 64. Следовательно, площадь будет равна 64 setjat (единица измерения площади).
Другими словами, диаметр равен 2r, а 1/9 радиуса равно (1/9 • 2r). Тогда если мы вычтем это из исходного диаметра, то получим 2r — (1/9 • 2r) = 8/9(2r). Тогда площадь круга равна 256/81 r². То есть пи равно почти 3,16. Они обнаружили это значение пи примерно 4000 лет назад.

Рисунок 26: математический папирус Ахмеса.

Однако греческие математики нашли для вычисления пи способ получше. Например, Архимед предпочитал работать с периметрами. Он начал рисовать окружности, описывающие многоугольники разного размера. Когда он чертил шестиугольник, то рисовал окружность с диаметром 1. Затем он видел что каждая сторона шестиугольника равна 1/2, а периметр шестиугольника равен 1/2 x 6 = 3. Затем он увеличивал количество сторон многоугольника, пока он не становился похожим на круг. Работая со 96-сторонним многоугольником и применив тот же способ, он получил 2 десятичных разряда пи после запятой: 3 и 10/71 = 3,14084. Спустя много лет китайский математик Лю Ху использовал 3072-сторонний многоугольник и получил число 3,14159 (5 верных десятичных разрядов числа пи после запятой). После этого ещё один китайский математик Цзу Чунчжи провёл ещё более впечатляющую работу. Он работал со 24000-сторонним многоугольником и получил 3,1415926 — семь верных десятичных разрядов пи после запятой.

Спустя тысячу лет немецкий математик Людольф Цейлен работал со 2⁶²-сторонним многоугольником и получил 35 десятичных разрядов пи. Это число, названное Людольфовым, было высечено на его могильном камне.

В 1706 году англичанин Джон Мэчин, долгое время работавший профессором астрономии, использовал формулу сложения, чтобы доказать, что пи равно
Не беспокоясь о том, как откуда взялась эта формула, Мэчин начал постоянно ею пользоваться, а затем записал показанный ниже ряд. Это был самый большой на то время шаг в количестве разрядов пи.
Рисунок 29: Формула Мэчина для пи

Однако первое упоминание пи появилось в 1706 году. Преподаватель математики Уильям Джонс написал книгу и впервые предложил пи для измерения окружностей. Так пи впервые появилась в книгах!

Рисунок 30: Juliabloggers

В 1873 году Уильям Шэнкс воспользовался формулой Джона Мэчина и получил 707 десятичных разрядов пи. Эти цифры написаны в комнате пи парижского Дворца открытий. Однако позже математики выяснили, что верными являются только 527 разрядов.

Рисунок 31: комната пи

С другой стороны, более интересный способ нахождения пи обнаружил Буффон. Его эксперимент основывался на случайном разбрасывании иголок для оценки пи. Он нарисовал на доске несколько параллельных линий на расстоянии D и взял иголки длиной L. Затем он случайным образом начал бросать иголки на доску и записывал долю иголок, пересекавших линию.

Рисунок 32.0: Science Friday

А после этого другой математик по имени Ладзарини подбросил иголку 3408 раз и получил шесть десятичных разрядов пи с соотношением 355/113. Однако если бы одна иголка не пересекла линию, он получил бы только 2 разряда пи.

Рисунок 32.1: бросание 1000 иголок для оценки приблизительного значения пи

e: история экспоненциального роста

e — это ещё одно знаменитое иррациональное число. Дробная часть e тоже бесконечна, как и у пи. Мы используем число e для вычисления степенного (экспоненциального) роста. Другими словами, мы используем e, когда видим очень быстрый рост или уменьшение.

Один из величайших, а возможно и лучший математик Леонард Эйлер открыл число e в 1736 году и впервые упомянул это особое число в своей книге Mechanica.

Рисунок 33: источник

Чтобы разобраться в экспоненциальном росте, мы можем использовать историю об изобретателе шахмат. Когда он придумал эту игру, то показал её властителю Севера. Царю понравилась игра и он пообещал, что отдаст автору любую награду. Тогда изобретатель попросил нечто очень простое: 2⁰ зерна на первую клетку шахматной доски, 2¹ зерна на вторую клетку доски, 2² зерна — на третью, и так далее. Каждый раз количество зерна удваивалось. Царь Севера подумал, что просьбу будет выполнить легко, но он ошибался, потому то на последнюю клетку нужно было бы положить 2⁶³ зёрен, что равно 9 223 372 036 854 775 808. Это и есть экспоненциальный рост. Он начался с 1, постоянно удваивался, и через 64 шага вырос в огромное число!

Если бы изобретатель шахмат выбрал линейное уравнение, например 2n, то получил бы 2, 4, 6, 8, … 128… Следовательно, в дальней перспективе экспоненциальный рост часто намного превышает полиномиальный.

Кстати, 9 223 372 036 854 775 808–1 — это максимальное значение 64-битного целого числа со знаком.

Рисунок 34: источник: Wikipedia

Число e открыл Эйлер. Однако Якоб Бернулли тоже работал с числом e, когда вычислял сложный процент, чтобы заработать больше денег. Если вложить 100 долларов под 10% дохода, то как будет расти эта сумма? Во-первых, это зависит от того, как часто банк рассчитывает проценты. Например, если он рассчитывает один раз, то мы получим в конце года 110 долларов. Если мы передумаем и будем брать проценты каждые 6 месяцев, то в этом случае мы получим больше 110 долларов. Дело в ттом, что процент, полученный за первые 6 месяцев, тоже получит свой процент. Общая сумма будет равна 110,25 долларов. Можно догадаться, что мы можем получить больше денег, если будем забирать деньги каждый квартал года. А если мы будем делать временной интервал всё короче, то окончательные суммы будут продолжать расти. Такой бесконечный сложный процент сделает нас богатыми! Однако наш общий доход стремится к ограниченному значению, связанному с e.

Бернулли не называл число 2,71828 именем e. Когда Эйлер работал с 2,71828, он возвёл экспоненциальную функцию e в степень x. Свои открытия он изложил в книге The Analysis of Infinite.

В 1798 году Томас Мальтус использовал экспоненциальную функцию в своём эссе, посвящённом пищевому дефициту будущего. Он создал линейный график, показывающий производство пищи и экспоненциальный график, показывающий население мира. Мальтус сделал вывод, что в дальней перспективе экспоненциальный рост победит, и мир ждёт серьёзный дефицит пищи. Это явление назвали «мальтузианской катастрофой». Ньютон тоже использовал эту модель, чтобы показать, как охлаждается чашка чая.

Рисунок 35: закон Ньютона-Рихмана
Рисунок 36: мальтузианская катастрофа

Мнимость числа: i, квадратный корень -1

Долгое время для решения своих задач математикам было достаточно обычных чисел. Однако в какой-то момент для дальнейшего развития им потребовалось открыть нечто новое и загадочное. Например, итальянский математик Кардано пытался разделить число 10 на 2 части, произведение которых было бы равно 40. Чтобы решить эту задачу, он записал уравнение: x (10-x) = 40. Когда он решил это квадратное уравнение, то получил два решения: 5 плюс √-15 и 5 минус √-15, что в то время не имело никакого смысла. Этот результат был бессмысленным, потому что по определению квадратного корня ему нужно было найти число, квадрат которого был бы отрицательным. Однако и положительное, и отрицательное числа в квадрате имеют положительное значение. Как бы то ни было, он нашёл своё уникальное число. Однако первым математиком, назвавшим √-1 (квадратный корень из минус единицы) мнимым числом i, был Эйлер.

Лейбниц дал такой комментарий о мнимом числе √-1:

Комплексные числа — это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием.

Мы можем складывать, вычитать, умножать и делить мнимые числа. Сложение, вычитание и умножение просты, а деление немного сложнее. Вещественные и мнимые части складываются по отдельности. В случае умножения i² будет равно -1.

После Эйлера математик Каспар Вессель представил мнимые числа геометрически с создал комплексную плоскость. Сегодня мы представляем каждое комплексное число a + bi как точку с координатами (a,b).

Рисунки 37 и 38: комплексные числа

В викторианскую эпоху многие относились к мнимым числам с подозрением. Однако ирландский математик и астроном Уильям Роуэн Гамильтон покончил с этими сомнениями, определив комплексные числа применительно к кватернионам.

Самое красивое уравнение: тождество Эйлера

Тождество Эйлера связывает экспоненциальную функцию с функциями синуса и косинуса, значения которых колеблются от минус единицы до единицы. Чтобы найти связь с тригонометрическими функциями, мы можем представить их в виде бесконечного ряда, истинного для всех значений

Рисунок 39: открытие тождества Эйлера

Рисунок 40: тождество Эйлера

Эйлер никогда не записывал это тождество в явном виде, и мы не знаем, кто впервые записал его. Тем не менее, мы связываем его с именем Эйлера в знак почтения перед этим великим первопроходцем математики.

Самое длинное слово в мире содержит 189 819 букв :: Инфониак

Невероятные факты Полное химическое название самого большого белка содержит 189 819 букв и считается самым длинным словом в любом языке.
Титин, также известный, как коннектин – это гигантский белок, состоящий из 244 индивидуально сложенных областей белка, соединенных неструктурированной последовательностью пептидов.
Кроме того, ген титина содержит самое большое количество экзонов – 363, обнаруженных в одном гене.
Титин играет важную роль в сокращении поперечно-полосатых мышечных тканей, но он больше всего известен своим техническим названием, которое считается самым длинным словом в любом языке мира.
Название «титин» заимствовано из греческого слова «titan» (гигантское божество, нечто большого размера). Химическое название начинается с метионил … и заканчивается …изолейцин.

Полное название самого большого белка заняло бы очень много места в данном посте, но вы можете прочесть его тут.
Если же вы действительно хотите услышать, как звучит самое длинное слово в мире, то можете посмотреть видео, которое занимает почти 3,5 часа для полного произнесения этого названия.

Интересно, что полное химическое название титина вы даже не увидите в словарях, так как составители словарей считают названия химических соединений вербальной формулой, а не словом. Но как бы вы это не называли: слово, формула или целая история, оно крайне длинное.

Самое длинное слово русского языка

Теоретически существуют слова с неограниченной длиной, такие как, например, «прапрапра…дедушка», так как в русском языке не существует ограничений для приставок «пра».
Одними из самых длинных слов являются те, что обозначают величины и конечно химические названия.
Самое длинное слово, обозначающее возраст:
«восьмидесятичетырёхлетний» (25 букв)
Самое длинное слово в Книге рекордов Гиннеса:
«превысокомногорассмотрительствующий»(35 букв) и
«рентгеноэлектрокардиографического» (33 буквы)
Самое длинное слово, обозначающее величину:
«тысячадевятьсотвосьмидесятидевятимиллиметровый » (47 букв)
Самое длинное слово, обозначающее химическое вещество:
«никотинамидадениндинуклеотидфосфатгидрин» (40 букв)
» Тетрагидропиранилциклопентилтетрагидропиридопиридиновые» (55 букв)
Слово, обозначающее боязнь длинных слов:
«гиппопотомонстросескиппедалофобия » (33 буквы)

Титин — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 октября 2019; проверки требуют 3 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 октября 2019; проверки требуют 3 правки.
Титин

Трёхмерная структура модуля титина I типа. PDB прорисовано на основе 1bpv.
Доступные структуры
PDB Поиск ортологов: PDBe, RCSB
Список идентификаторов PDB
1BPV, 1G1C, 1NCT, 1NCU, 1TIT, 1TIU, 1TKI, 1TNM, 1TNN, 1WAA, 1YA5, 2A38, 2BK8, 2F8V, 2ILL, 2J8H, 2J8O, 2NZI, 2RQ8, 2WP3, 2WWK, 2WWM, 2Y9R, 3B43, 3KNB, 3LCY, 3LPW, 3PUC, 3Q5O, 3QP3, 4JNW
Идентификаторы
Символ TTN ; CMD1G; CMH9; CMPD4; EOMFC; HMERF; LGMD2J; MYLK5; TMD
Внешние ID OMIM: 188840 MGI: 98864 HomoloGene: 130650 GeneCards: TTN Gene
номер EC 2.7.11.1
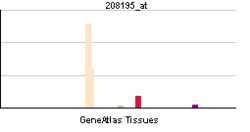
Профиль экспрессии РНК
Больше информации
Ортологи
Вид Человек Мышь
Entrez 7273 22138
Ensembl ENSG00000155657 ENSMUSG00000051747
UniProt Q8WZ42 A2ASS6
RefSeq (мРНК) NM_001256850 NM_011652
RefSeq (белок) NP_001243779 NP_035782
Локус (UCSC) Chr 2:
179.39 – 179.7 Mb Chr 2:
76.7 – 76.98 Mb
Поиск в PubMed [1] [2]
Титин, также известный как коннектин — самый большой из одиночных полипептидов. Он играет важную роль в процессе сокращения поперечнополосатых мышц^[1]^[2]. Ген титина содержит самое большое количество экзонов.
Титин, состоящий из 38138 аминокислот (титин камбаловидной мышцы) — самый большой из известных белков. Молекулярная масса белка равна приблизительно 2 993 442.763 а. е. м.^[3], его теоретическая изоэлектрическая точка равна 6.01^[4]. Эмпирическая химическая формула этого белка — C₁₃₂₉₈₃H₂₁₁₈₆₁N₃₆₁₄₉O₄₀₈₈₃S₆₉₃. Теоретический нестабильный индекс (II), показывающий его стабильность в пробирке, равен 39.69. Период полураспада (время, требующееся для исчезновения половины содержащегося белка в клетке после его синтеза) равен примерно 30 часам (в ретикулоцитах животных)^[5]. Титин состоит главным образом из линейных блоков модулей двух типов: тип I (фибронектиновый домен III типа) и тип II (иммуноглобулиноподобный домен)^[6]. Эти линейные блоки далее организуются в два участка:
N-терминальный (в составе I-полос саркомера)
действует как эластичная часть молекулы и состоит, в основном, из модулей типа II. В частности, I группа состоит из двух участков тандемных иммуноглобулиновых доменов типа II на каждой стороне PEVK- участка, богатых пролином, глутаминовой кислотой, валином и лизином. Располагается между миозином и Z-диском^[7].
C-терминальный (в составе А-полос)
выполняет управляющую функцию и, вероятно, обладает протеинкиназной активностью. А-полосы состоят из чередующихся модулей типа I и типа II.
Титин — это большой белок поперечно-полосатых мышц. N-терминальный участок Z-диска и C-терминальный участок М-линии связаны, соответственно, с Z-диском и М-линией саркомера, так что одиночная молекула титина тянется вдоль половины его длины. Титин также содержит скрепляющие участки для присоединения мышечных белков, так что он служит матрицей для правильной сборки белков, входящих в состав саркомера. Было установлено, что он также входит в качестве структурного белка в состав хромосом. Значительная изменчивость характерна для участков молекулы титина, находящихся в I-полосе, М-линии, Z-диске. Изменчивость в участке I-полосы определяет различия в эластичности разных изоформ титина, и, следовательно, различия в эластичности разных типов мускулов. Из многих известных вариантов титина только для пяти из них полностью расшифрована последовательность аминокислот^[2]^[8].
Титин взаимодействует с множеством саркомерных белков, включая:^[9]
Z-линейный участок: телетонин и α-актинин-1
Участок I-полосы: калпейн-3 и обскурин
М-линейный участок: миозин-связующий белок С, кальмодулин 1, калпеин-3 и Убиквитинлигаза.
Мутации в гене титина связаны с наследственной гипертрофической кардиомиопатией^[10]^[11] и прогрессирующей дистальной мышечной дистрофией Миоши^[12]. Аутоантитела против титина вырабатываются у больных аутоиммунной склеродермией^[13].
Как у самого большого известного белка, у титина самое длинное номенклатурное название ИЮПАК. Полное химическое название, начинающееся метионил… и заканчивающееся …изолейцин, включает (на английском языке) 189 819 букв, признано длиннейшим словом не только в английском языке, но и в любом другом^[14]. Однако профессиональные составители словарей рассматривают названия химических соединений скорее как словесные химические формулы, нежели как слова общеупотребительного языка^[15].
↑ OMIM 188840
↑ ¹ ² Entrez Gene: TTN titin (неопр.).
↑ Result of Molecular Weight Calculation
↑ ExPASy-calculated pI for titin (неопр.). Дата обращения 26 августа 2007. Архивировано 13 апреля 2012 года.
↑ Swiss-Prot Protein knowledgebase, main entry (неопр.). Дата обращения 4 мая 2006. Архивировано 13 апреля 2012 года.
↑ Labeit S., Kolmerer B. Titins: giant proteins in charge of muscle ultrastructure and elasticity (англ.) // Science : journal. — 1995. — October (vol. 270, no. 5234). — P. 293—296. — PMID 7569978.
↑ Wang K., McCarter R., Wright J., Beverly J., Ramirez-Mitchell R. Regulation of skeletal muscle stiffness and elasticity by titin isoforms: a test of the segmental extension model of resting tension (англ.) // Proceedings of the National Academy of Sciences of the United States of America : journal. — 1991. — August (vol. 88, no. 16). — P. 7101—7105. — PMID 1714586.
↑ Labeit S., Barlow D.P., Gautel M., Gibson T., Holt J., Hsieh C.L., Francke U., Leonard K., Wardale J., Whiting A., Trinick J. A regular pattern of two types of 100-residue motif in the sequence of titin (англ.) // Nature : journal. — 1990. — May (vol. 345, no. 6272). — P. 273—276. — DOI:10.1038/26926a0. — PMID 2129545.
↑ Bang M.L., Centner T., Fornoff F., Geach A.J., Gotthardt M., McNabb M., Witt C.C., Labeit D., Gregorio C.C., Granzier H., Labeit S. The complete gene sequence of titin, expression of an unusual approximately 700-kDa titin isoform, and its interaction with obscurin identify a novel Z-line to I-band linking system (англ.) // Circ. Res. (англ.)русск. : journal. — 2001. — November (vol. 89, no. 11). — P. 1065—1072. — DOI:10.1161/hh3301.100981. — PMID 11717165. (недоступная ссылка)
↑ Siu B.L., Niimura H., Osborne J.A., Fatkin D., MacRae C., Solomon S., Benson D.W., Seidman J.G., Seidman C.E. Familial dilated cardiomyopathy locus maps to chromosome 2q31 (англ.) // Circulation (англ.)русск. : journal. — Lippincott Williams & Wilkins (англ.)русск., 1999. — March (vol. 99, no. 8). — P. 1022—1026. — PMID 10051295.
↑ Itoh-Satoh M., Hayashi T., Nishi H., Koga Y., Arimura T., Koyanagi T., Takahashi M., Hohda S., Ueda K., Nouchi T., Hiroe M., Marumo F., Imaizumi T., Yasunami M., Kimura A. Titin mutations as the molecular basis for dilated cardiomyopathy (англ.) // Biochem. Biophys. Res. Commun. (англ.)русск. : journal. — 2002. — February (vol. 291, no. 2). — P. 385—393. — DOI:10.1006/bbrc.2002.6448. — PMID 11846417.
↑ Hackman P., Vihola A., Haravuori H., Marchand S., Sarparanta J., De Seze J., Labeit S., Witt C., Peltonen L., Richard I., Udd B. Tibial muscular dystrophy is a titinopathy caused by mutations in TTN, the gene encoding the giant skeletal-muscle protein titin (англ.) // Am. J. Hum. Genet. (англ.)русск. : journal. — 2002. — September (vol. 71, no. 3). — P. 492—500. — DOI:10.1086/342380. — PMID 12145747.
↑ Machado C., Sunkel C.E., Andrew D.J. Human autoantibodies reveal titin as a chromosomal protein (англ.) // J. Cell Biol. (англ.)русск. : journal. — 1998. — April (vol. 141, no. 2). — P. 321—333. — DOI:10.1083/jcb.141.2.321. — PMID 9548712.
↑ What is the longest word in the English language? (неопр.). CliffsNotes.com. Дата обращения 24 января 2016.
↑ Oxford Word and Language Service team. Ask the experts — What is the longest English word? (неопр.). AskOxford.com / Oxford University Press. Дата обращения 13 января 2008. Архивировано 13 апреля 2012 года.
Самое длинное в мире слово

Самое длинное официальное название — холм высотой 305 метров, находящийся в Новой Зеландии.
Mamihlapinatapai (иногда пишут mamihlapinatapei) — слово из языка племени Яган (Огненная Земля). Оно указано в Книге рекордов Гиннесса в качестве «наиболее сжатого слова» и считается одним из самых трудных для перевода слов.
Mamihlapinatapai означает «Взгляд между двумя людьми, в котором выражается желание каждого в том, что другой станет инициатором того, чего хотят оба, но ни один не хочет быть первым».
А вот какое самое длинное в мире слово?

Полное химическое название самого большого белка содержит 189 819 букв и считается самым длинным словом в любом языке.
Титин, также известный, как коннектин – это гигантский белок, состоящий из 244 индивидуально сложенных областей белка, соединенных неструктурированной последовательностью пептидов.
Кроме того, ген титина содержит самое большое количество экзонов – 363, обнаруженных в одном гене.
Титин играет важную роль в сокращении поперечно-полосатых мышечных тканей, но он больше всего известен своим техническим названием, которое считается самым длинным словом в любом языке мира.
Название «титин» заимствовано из греческого слова «titan» (гигантское божество, нечто большого размера). Химическое название начинается с метионил … и заканчивается …изолейцин.
Полное название самого большого белка заняло бы очень много места в данном посте, но вы можете прочесть его тут.
Если же вы действительно хотите услышать, как звучит самое длинное слово в мире, то можете посмотреть видео, которое занимает почти 3,5 часа для полного произнесения этого названия.
Интересно, что полное химическое название титина вы даже не увидите в словарях, так как составители словарей считают названия химических соединений вербальной формулой, а не словом. Но как бы вы это не называли: слово, формула или целая история, оно крайне длинное.
Самое длинное слово в русском языке до сих пор не определено по ряду причин. Теоретически одним из таких слов может являться прилагательное тетрагидропиранилциклопентилтетрагидропиридопиридиновые, состоящее из 55 букв. Но будет ли справедливым такой выбор победителя, ведь в аналитической, предположим, химии, наименования веществ могут строиться по определённой схеме и порою достигать прямо таки космических величин.
Также часто приводимым примером является построение слова методом добавления приставки пра-. Её количество может быть неограниченным, следовательно, букв в таком слове будет предостаточно.
Популярными являются и различные слова, содержащие в себе числительное и обозначающие какую-либо величину — тысячавосемьсотсемидесятидевятисантиметровый, или построенные по типу восьмидесятичетырёхлетний. Для указания возраста, например, Земли. Так что возможностей для словотворчества бессчётное количество. Комбинировать варианты можно довольно долго, ведь, как мы знаем, натуральных чисел тьма. То бишь можно задаться выражением диаметра Земли в миллиметрах, и Вы можете только вообразить, сколько букв будет в этом новорожденном слове. Ввиду этого задача по нахождению длиннейшего слова в русском языке, увы, не увенчается успехом. Тем паче, что большинство подобных слов обывателю кажется едва ли не монстром, и в обычной речи совсем не употребляются. Разве что в локальных масштабах. То есть вполне возможно найти самое длинное слово среди частей речи, к примеру, глаголов или существительных.
Некоторые трудности создаёт и отсутствие договорённости о том, можно ли использовать различные словоформы. Так, например, в Книге рекордов Гиннесса в 1993 году самым длинным словом названо было слово рентгеноэлектрокардиографического (33 буквы), в издании 2003 года — превысокомногорассмотрительствующий (35 букв). В первом случае мог быть употреблён и аналог слова — энтерогематогепатогематопульмоэнтерального (42 буквы). Споры возникали, естественно, по причине того, что, как мы можем видеть, в первом случае слово употреблено в родительном падеже, а во втором вариант написания, например, в том же падеже, был бы длиннее на букву. В общем, слова-рекордсмены так и не удостоились быть признанными, ведь сведения носят довольно субъективный характер и не могут быть подтверждены.
А как Вам такая самая длинная аббревиатура? (56 символов)
HИИОМТПЛАБОПАРМБЕТЖЕЛБЕТРАБСБОРМОHИМОHКОH-ОТДТЕХСТРОМОHТ
Научно-исследовательская лаборатория операций по армированию бетона и железобетонных работ по сооружению сборно-монолитных и монолитных конструкций отдела технологии строительно-монтажного управления Академии строительства и архитектуры СССР. То есть можете себе представить, как сотрудники данной организации отвечали на вопрос о работе.
Теперь поговорим о самых-самых в своём роде.
Самое длинное прилагательное с дефисом: сельскохозяйственно-машиностроительный (38 букв).
Самые длинные существительные с дефисом: корчеватель-бульдозер-погрузчик и одушевлённость-неодушевлённость (31 буква).
Самое длинное существительное без дефиса: водогрязеторфопарафинолечение (29 букв).
Самое длинное прилагательное без дефиса: электрофотополупроводниковый (28 букв). Эти данные любезно предоставлены орфографическим словарём Российской академии наук.
Грамматический словарь А.А.Зализняка, изданный в 2003 году считает, что : самая длинная (в буквах) нарицательная лексема в словарной форме — прилагательное частнопредпринимательский (25 букв; словоформы на -ого и -ими — 26 букв).
Самые длинные глаголы — переосвидетельствоваться, субстанционализироваться и интернационализироваться .(все — 24 буквы; образованные от них причастия с окончанием -ующимися и деепричастия на -овавшись — по 25 букв). С первого раза даже не сразу смогла представить смысл второго слова…
Самые длинные существительные — человеконенавистничество и высокопревосходительство (по 24 буквы; словоформы на -ами — по 26 букв)
Самые длинные одушевлённые существительные — одиннадцатиклассница (20 букв) и делопроизводительница (21 буква), словоформы на -ами — по 22 и 23 буквы соответственно.
Самое длинное наречие, фиксируемое словарём, — неудовлетворительно (19 букв). Не стоит забывать, что от подавляющего большинства качественных прилагательных на -ый и -ий образуются наречия на -о, -е или -и, далеко не всегда фиксируемые словарём.
Самое длинное междометие, включённое в словарь, — немного грубое физкульт-привет (14 букв).
Слово соответственно (14 букв) является одновременно самым длинным предлогом. Самая длинная частица исключительно на букву короче.
Но помимо длинных,малоизвестных и узкоспециализированных слов, встречаются и чемпионы в литературе, например, слово попреблагорассмотрительствующемуся, которое Николай Лесков употребил в рассказе «Заячий ремиз».Самое интересное, что доподлинного значения никто не знает,вполне вероятно,что автор его сам и придумал. Но, наверное, каждый может представить для себя его значение.
Много еще интересного скрывает наш язык, и, думаю, количество слов-рекордсменов никак не влияет на мощь и красоту нашей русской речи. Собирая информацию для этой статьи, узнала невероятно много любопытных вещей. И почему-то вспомнилось, что лет в семь думалось, что слово электросинхрофазотрон — ну самое длинное, а улица Старопортофранковская — вообще что-то из разряда фантастики. Убеждения меняются…А главное, язык не является чем-то статичным, и ежедневно пополняется неологизмами; он живёт, перерождается, и неизвестно, какой длины может стать слово-чемпион.Хотя, судя по нынешнему стремлению юных укоротить слово до неузнаваемости, ещё неведомо, кто победит…
А когда я учился в институте, у нас в группе был студент, который считал свою фамилию самой длинной в России — Скоробогатько — 13 букв, у кого больше?
Самые красивые физические и математические формулы.: moris_levran — LiveJournal

Математик Анри Пуанкаре в книге «Наука и метод» писал: «Если бы природа не была прекрасна, она не стоила бы того, чтобы ее знать, жизнь не стоила бы того, чтобы ее переживать. Я здесь говорю, конечно, не о той красоте, которая бросается в глаза… Я имею в виду ту более глубокую красоту, которая открывается в гармонии частей, которая постигается только разумом. Это она создает почву, создает каркас для игры видимых красок, ласкающих наши чувства, и без этой поддержки красота мимолетных впечатлений была бы несовершенна как все неотчетливое и преходящее. Напротив красота интеллектуальная дает удовлетворение сама по себе».
П.А.М. Дирак писал: «У теоретической физики есть еще один верный путь развития. Природе присуща та фундаментальная особенность, что самые основные физические законы описываются математической теорией, аппарат которой обладает необыкновенной силой и красотой. Чтобы понять эту теорию, нужно обладать необычайно высокой математической квалификацией. Вы можете спросить: почему природа устроена именно так? На это можно ответить только одно: согласно нашим современным знаниям, природа устроена именно так, а не иначе».

Семь лет назад украинский физик (и художник) Наталия Кондратьева обратилась к ряду ведущих математиков мира с вопросом: «Какие три математические формулы, на ваш взгляд, самые красивые?»
В беседе о красоте математических формул приняли участие сэр Михаэль Атья и Дэвид Элварси из Британии, Яков Синай и Александр Кириллов из США, Фридрих Херцебрух и Юрий Манин из Германии, Давид Рюэль из Франции, Анатолий Вершик и Роберт Минлос из России и другие математики из разных стран. Из украинцев в дискуссии приняли участие академики НАНУ Владимир Королюк и Анатолий Скороход. Часть полученных таким образом материалов и легла в основу изданной Натальей Кондратьевой научной работы «Три самые красивые математические формулы».
— Какую цель вы ставили, обращаясь к математикам с вопросом о красивых формулах?
— Каждое новое столетие приносит обновление научной парадигмы. В самом начале века с ощущением, что мы стоим у порога новой науки, ее новой роли в жизни человеческого общества, я обратилась к математикам с вопросом о красоте идей, стоящих за математическими символами, т.е. о красоте математических формул.
Уже сейчас можно отметить некоторые особенности новой науки. Если в науке ХХ века очень важную роль играла «дружба» математики с физикой, то сейчас математика эффективно сотрудничает с биологией, генетикой, социологией, экономикой… Следовательно, наука будет исследовать соответствия. Математические структуры будут исследовать соответствия между взаимодействиями элементов различных областей и планов. И многое, что раньше мы воспринимали на веру как философские констатации, будет утверждено наукой как конкретное знание.
Этот процесс начался уже в ХХ веке. Так, Колмогоров математически показал, что случайности нет, а есть очень большая сложность. Фрактальная геометрия подтвердила принцип единства в многообразии и т.д.
— Какие же формулы были названы самыми красивыми?
— Сразу скажу, что цели устроить конкурс формулам не было. В своем письме к математикам я писала: «Люди, которые хотят понять, какими законами управляется мир, становятся на путь отыскания гармонии мира. Путь этот уходит в бесконечность (ибо движение вечно), но люди всё равно идут им, т.к. есть особая радость встретить очередную идею или представление. Из ответов на вопрос о красивых формулах, возможно, удастся синтезировать новую грань красоты мира. Кроме того, эта работа может оказаться полезной для будущих ученых как мысль о великой гармонии мира и математики как способе отыскания этой красоты».
Тем не менее среди формул оказались явные фавориты: формула Пифагора и формула Эйлера.
Вслед за ними расположились скорее физические, чем математические формулы, которые в ХХ веке изменили наше преставление о мире, —Максвелла, Шредингера, Эйнштейна.
Также в число самых красивых попали формулы, которые еще находятся на стадии дискуссии, такие, например, как уравнения физического вакуума. Назывались и другие красивые математические формулы.
— Как вы думаете, почему на рубеже второго и третьего тысячелетий формула Пифагора названа одной из самых красивых?
— Во времена Пифагора эта формула воспринималась как выражение принципа космической эволюции: два противоположных начала (два квадрата, соприкасающихся ортогонально) порождают третье, равное их сумме. Можно дать геометрически очень красивые интерпретации.
Возможно, существует какая-то подсознательная, генетическая память о тех временах, когда понятие «математика» означало — «наука», и в синтезе изучались арифметика, живопись, музыка, философия.
Рафаил Хасминский в своем письме написал, что в школе он был поражен красотой формулы Пифагора, что это во многом определило его судьбу как математика.
— А что можно сказать о формуле Эйлера?
— Некоторые математики обращали внимание, что в ней «собрались все», т.е. все самые замечательные математические числа, и единица таит в себе бесконечности! — это имеет глубокий философский смысл.
Недаром эту формулу открыл Эйлер. Великий математик много сделал, чтобы ввести красоту в науку, он даже ввел в математику понятие «градус красоты». Вернее, он ввел это понятие в теорию музыки, которую считал частью математики.
Эйлер полагал, что эстетическое чувство можно развивать и что это чувство необходимо ученому.
Сошлюсь на авторитеты… Гротендик: «Понимание той или иной вещи в математике настолько совершенно, насколько возможно прочувствовать ее красоту».
Пуанкаре: «В математике налицо чувство». Он сравнивал эстетическое чувство в математике с фильтром, который из множества вариантов решения выбирает наиболее гармоничный, который, как правило, и есть верный. Красота и гармония — синонимы, а высшее проявление гармонии есть мировой закон Равновесия. Математика исследует этот закон на разных планах бытия и в разных аспектах. Недаром каждая математическая формула содержит знак равенства.
Думаю, что высшая человеческая гармония есть гармония мысли и чувства. Может быть, поэтому Эйнштейн сказал, что писатель Достоевский дал ему больше, чем математик Гаусс.
Формулу Достоевского «Красота спасет мир» я взяла в качестве эпиграфа к работе о красоте в математике. И он также обсуждался математиками.
— И они согласились с этим утверждением?
— Математики не утверждали и не опровергали этого утверждения. Они его уточнили: «Осознание красоты спасет мир». Здесь сразу вспомнилась работа Юджина Вигнера о роли сознания в квантовых измерениях, написанная им почти пятьдесят лет назад. В этой работе Вигнер показал, что человеческое сознание влияет на окружающую среду, т.е., что мы не только получаем информацию извне, но и посылаем наши мысли и чувства в ответ. Эта работа до сих пор актуальна и имеет как своих сторонников, так и противников. Я очень надеюсь, что в ХХI веке наука докажет: осознание красоты способствует гармонизации нашего мира.
1. Формула Эйлера. Многие видели в этой формуле символ единства всей математики, ибо в ней «-1 представляет арифметику, i — алгебру, π — геометрию и e — анализ».

2. Это простое равенство показывает, величина 0,999 (и так до бесконечности) эквивалентна единице. Многие люди не верят, что это может быть правдой, хотя существует несколько доказательств, основанных на теории пределов. Тем не менее, равенство показывает принцип бесконечности.

3. Это уравнение было сформулировано Эйнштейном в рамках новаторской общей теории относительности в 1915 году. Правая часть этого уравнения описывает энергию, содержащуюся в нашей Вселенной (в том числе» темную энергию»). Левая сторона описывает геометрию пространства-времени. Равенство отражает тот факт, что в общей теории относительности Эйнштейна, масса и энергия определяют геометрию, и одновременно кривизну, которая является проявлением гравитации. Эйнштейн говорил, что левая часть уравнений тяготения в общей теории относительности, содержащая гравитационное поле, красива и как будто вырезана из мрамора, в то время как правая часть уравнений, описывающая материю, всё ещё уродлива, будто сделана из обыкновенной деревяшки.

4. Еще одна доминирующая теория физики — Стандартная модель — описывает электромагнитное, слабое и сильное взаимодействие всех элементарных частиц. Некоторые физики считают, что она отображает все процессы, происходящие во Вселенной, кроме темной материи, темной энергии и не включает в себя гравитацию. В Стандартную модель вписывается и неуловимый до прошлого года бозон Хиггса, хотя не все специалисты уверены в его существовании.

5. Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Ее мы помним еще со школы и считаем, что автор теоремы — Пифагор. На самом деле этой формулой пользовались еще в Древнем Египте при строительстве пирамид.

6. Теорема Эйлера. Эта теорема заложила фундамент нового раздела математики — топологии. Уравнение устанавливает связь между числом вершин, ребер и граней для многогранников, топологически эквивалентных сфере.

7. Специальная теория относительности описывает движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. Эйнштейн составил формулу, которая описывает, что время и пространство не являются абсолютными понятиями, а скорее являются относительными в зависимости от скорости наблюдателя. Уравнение показывает, как расширяется или замедляется время в зависимости от того, как и куда движется человек.

8. Уравнение было получено в 1750-х годах Эйлером и Лагранжем при решении задачи об изохроне. Это проблема определения кривой, по которой тяжелая частица попадает в фиксированную точку за фиксированное время, независимо от начальной точки. В общих словах, если ваша система имеет симметрию, есть соответствующий закон сохранения симметрии.

9. Уравнение Каллана — Симанзика. Оно представляет собой дифференциальное уравнение, описывающее эволюцию н-корреляционной функции при изменении масштаба энергий, при которых теория определена и включает в себя бета-функции теории и аномальные размерности. Это уравнение помогло лучше понять квантовую физику.

10. Уравнение минимальной поверхности. Это равенство объясняет формирование мыльных пузырей.

11. Прямая Эйлера. Теорема Эйлера была доказана в 1765 году. Он обнаружил, что середины сторон треугольника и основания его высот лежат на одной окружности.

12. В 1928 году П.А.М. Дирак предложил свой вариант уравнения Шредингера – которое соответствовало теории А. Эйнштейна. Учёный мир был потрясён – Дирак открыл своё уравнение для электрона путём чисто математических манипуляций с высшими математическими объектами, известными как спиноры. И это было сенсацией – до сих пор все великие открытия в физике должны стоять на прочной базе экспериментальных данных. Но Дирак считал, что чистая математика, если она достаточно красива, является надёжным критерием правильности выводов. «Красота уравнений важнее, чем их соответствие экспериментальным данным. … Представляется, что если стремишься получить в уравнениях красоту и обладаешь здоровой интуицией, то ты на верном пути». Именно благодаря его выкладкам был открыт позитрон – антиэлектрон, и предсказал наличие у электрона «спина» — вращения элементарной частицы.

13. Дж. Максвелл получил удивительные уравнения, объединившие все явления электричества, магнетизма и оптики. Замечательный немецкий физик, один из создателей статистической физики, Людвиг Больцман, сказал об уравнениях Максвелла: «Не Бог ли начертал эти письмена?»

14. Уравнение Шредингера.Уравнение, описывающее изменение в пространстве и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах. Играет в квантовой механике такую же важную роль, как уравнение второго закона Ньютона в классической механике.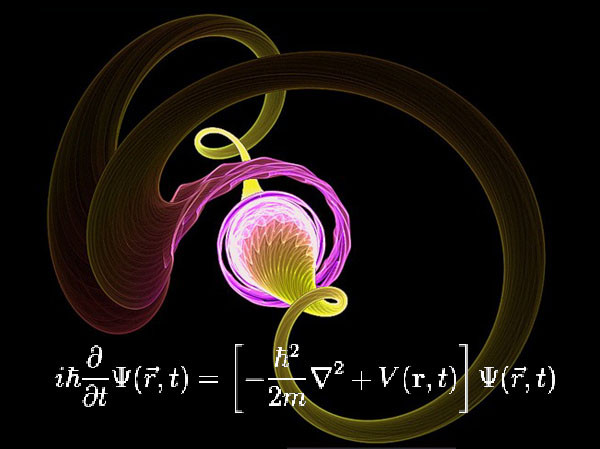
Химические рекорды
Главное меню » ЗНАЕТЕ ЛИ ВЫ, ЧТО… » Химические рекорды

Представляем подборку химических рекордов из Книги рекордов Гиннесса.
В связи с тем, что постоянно открываются новые вещества, данная подборка не является постоянной.

Химические рекорды для неорганических веществ
Самым распространенный элемент в земной коре — кислород O. Его весовое содержание составляет 49% от массы земной коры.
Самый редкий элемент в земной коре — астат At. Его содержание во всей земной коре составляет всего 0,16 гр. Второе место по редкости занимает франций Fr.
Самым распространенный элемент во вселенной — водород Н. Примерно 90% всех атомов во вселенной — это водород. Второе место по распространенности во вселенной занимает гелий He.
Самый сильный стабильный окислитель — комплекс дифторида криптона и пентафторида сурьмы. Из-за сильного окисляющего действия (окисляет почти все элементы в высшие степени окисления, в том числе окисляет кислород воздуха) для него очень трудно измерить электродный потенциал. Единственный растворитель, который реагирует с ним достаточно медленно — безводный фтористый водород.
Самое плотное вещество на планете Земля — осмий. Плотность осмия равна 22,587 г/см³.
Самый легкий металл — литий Li. Плотность лития равна 0,543 г/см³.
Самым плотным соединением является карбид дивольфрама W₂C. Плотность карбида дивольфрама составляет 17,3 г/см³.
В настоящее время твердым веществом с наименьшей плотностью являются графеновые аэрогели. Они представляют из себя систему из графен и нанотрубок заполненных воздушными прослойками. Самый легкий из таких аэрогелей имеет плотность 0,00016 г/см³. Предыдущее твердое вещество с наименьшей плотностью — кремниевый аэрогель (0,005 г/см³). Кремниевый аэрогель используют при сборе микрометеоритов, присутствующих в хвостах комет.
Самым легкий газ и, одновременно, самый легким неметалл — это водород. Масса 1 литра водорода равна всего 0,08988 гр. Ко всему прочему, водород также самый легкоплавкий неметалл при обычном давлении (температура плавления равна -259,19 ⁰С).
Самая легкая жидкость — жидкий водород. Масса 1 литра жидкого водорода составляет всего 70 грамм.
Самым тяжелым неорганическим газом при комнатной температуре, является гексафторид вольфрама WF₆(температура кипения равна +17 ⁰C). Плотность гексафторида вольфрама в виде газа составляет 12,9 г/л. Среди газов с температурой кипения ниже 0 °C рекорд принадлежит гексафториду теллура TeF₆ с плотностью газа при 25 ⁰С 9,9 г/л.
Самый дорогой металл в мире — калифорний Cf. Цена 1 грамма изотопа ²⁵²Cf доходит до 500 тыс. долларов США.
Гелий He является веществом с наименьшей температурой кипения. Его температура кипения равна -269 ⁰С. Гелий — единственное вещество не имеющее температуры плавления при обычном давлении. Даже при абсолютном нуле он остается жидким и может быть получен в твердом виде только под давлением (3 МПа).
Самый тугоплавкий металл и вещество с наибольшей температурой кипения — вольфрам W. Температура плавления вольфрама составляет +3420 ⁰С, а температура кипения +5680 ⁰С.
Самый тугоплавкий материал — это сплав карбидов гафния и тантала (1:1) (температура плавления +4215 ⁰С)
Самым легкоплавкий металл — ртуть. Температура плавления ртути равна -38,87 ⁰С. Ртуть также является самой тяжелой жидкостью, плотность при 25°C составляет 13,536 г/см³.
Самым стойким к кислотам металлом является иридий. До сих пор не известно ни одной кислоты или их смеси, в которых растворялся бы иридий. Однако его можно растворить в щелочах с окислителями.
Самой сильной стабильной кислотой является раствор пентафторида сурьмы во фтористом водороде.
Самым твердым металлом является хром Cr.
Самым мягким металлом при 25 ⁰C является цезий.
Самым твердым материалом по прежнему является алмаз, хотя имеется уже около десятка веществ приближающихся к нему по твердости (карбид и нитрид бора, нитрид титана и т.д.).
Самым электропроводным металлом при комнатной температуре является серебро Ag.
Самая низкая скорость звука в жидком гелии при температуре 2,18 К, она составляет всего 3,4 м/с .
Самая высокая скорость звука в алмазе — 18600 м/с.
Изотоп с самым коротким периодом полураспада это Li-5, который распадается за 4,4·10-22 секунды (выброс протона). Из-за столь малого времени жизни не все ученые признают факт его существования.
Изотоп с самым длинным измеренным периодом полураспада это Te-128, его период полураспада составляет 2,2·1024 лет (двойной β-распад).
Наиболее число стабильных изотопов имеют ксенон и цезий (по 36).
Самыми короткими названиями химического элемента обладают бор и иод (по 3 буквы).
Самыми длинными названиями химического элемента (по одиннадцать букв) обладают протактиний Pa, резерфордий Rf, дармштадтий Ds.
Химические рекорды для органических веществ
Самым тяжелым органическим газом при комнатной температуре и самым тяжелым газом среди всех при комнатной температуре, является N-(октафторбут-1-илиден)-O-трифторметилгидроксиламин (т. кип. +16 С). Его плотность в виде газа составляет 12,9 г/л. Среди газов с температурой кипения ниже 0°C рекорд принадлежит перфторбутану с плотностью газа при 0°С 10,6 г/л.
Самым горьким веществом является денатония сахаринат. Сочетание денатония бензоата с натриевой солью сахарина дало вещество в 5 раз более горькое, чем предыдущий рекордсмен (денатония бензоат).
Самым нетоксичным органическим веществом является метан. При увеличении его концентрации интоксикация возникает из-за недостатка кислорода, а не в результате отравления.
Самый сильный адсорбент для воды, был получен в 1974 году из производного крахмала, акриламида и акриловой кислоты. Это вещество способно удерживать воду, масса которой в 1300 раз превосходит его собственную.
Самый сильный адсорбент для нефтепродуктов — это углеродный аэрогель. 3,5 кг этого вещества способно поглотить 1 тонну нефти.
Самыми зловонными соединениями, являются этилселенол и бутилмеркаптан – их запах напоминает комбинацию запахов гниющей капусты, чеснока, лука и нечистот одновременно.
Самым сладким веществом, является N-((2,3-метилендиоксифенилметиламино)-(4-цианофенилимино)метил)аминоуксусная кислота (lugduname). Это вещество в 205 000 раз превосходит по сладости 2% раствор сахарозы. Существует несколько его аналогов с аналогичной сладостью. Из промышленных веществ самым сладким является талин (комплекс тауматина и солей алюминия), который в 3 500 — 6 000 раз слаще сахарозы. В последнее время в пищевой промышленности появился неотам обладающий сладостью в 7000 раз выше сахарозы.
Самым медленным ферментом, является нитрогеназа, катализирующая усвоение клубеньковыми бактериями атмосферного азота. Полный цикл превращения одной молекулы азота в 2 иона аммония занимает полторы секунды.
Органическим веществом с самым большим содержанием азота является либо бис(диазотетразолил)гидразин C2h3N12, содержащий 86,6% азота, либо тетраазидометан C(N3)4, содержащий 93,3% азота (зависит от того, считать ли последнее вещество органическим или нет). Это взрывчатые вещества, черезвычайно чувствительные к удару, трению и теплу. Из неорганических веществ рекорд конечно принадлежит газообразному азоту, а из соединений — азотистоводородной кислоте HN₃.
Самое длинное химическое название насчитывает 1578 знаков в английском написании и является модифицированной нуклеотидной последовательностью. Это вещество называется: Adenosene. N-[4-(dimethylethyl)benzoyl]-2′-O-(tetrahydromethoxypyranyl)adenylyl-(3’→5′)-4-deamino-4-(2,4-dimethylphenoxy)-2′-O-(tetrahydromethoxypyranyl)cytidylyl-(3’→5′)-4-deamino-4-(2,4-dimethylphenoxy)-2′-O-(tetrahydromethoxypyranyl)cytidylyl-(3’→5′)-N-[4-(dimethylethyl)benzoyl]-2′-O-(tetrahydromethoxypyranyl)cytidylyl-(3’→5′)-N-[4-(dimethylethyl)benzoyl]-2′-O-(tetrahydromethoxypyranyl)cytidylyl-(3’→5′)-N-[[4-(dimethylethyl)phenyl]acetyl]-2′-O-(tetrahydromethoxypyranyl)guanylyl-(3’→5′)-N-[[4-(dimethylethyl)phenyl]acetyl]-2′-O-(tetrahydromethoxypyranyl)guanylyl-(3’→5′)-N-[4-(dimethylethyl)benzoyl]-2′-O-(tetrahydromethoxypyranyl)adenylyl-(3’→5′)-N-[4-(dimethylethyl)benzoyl]-2′-O-(tetrahydromethoxypyranyl)cytidylyl-(3’→5′)-4-deamino-4-(2,4-dimethylphenoxy)-2′-O-(tetrahydromethoxypyranyl)cytidylyl-(3’→5′)-4-deamino-4-(2,4-dimethylphenoxy)-2′-O-(tetrahydromethoxypyranyl)cytidylyl-(3’→5′)-N-[[4-(dimethylethyl)phenyl]acetyl]-2′-O-(tetrahydromethoxypyranyl)guanylyl-(3’→5′)-4-deamino-4-(2,4-dimethylphenoxy)-2′-O-(tetrahydromethoxypyranyl)cytidylyl-(3’→5′)-N-[4-(dimethylethyl)benzoyl]-2′-O-(tetrahydromethoxypyranyl)cytidylyl-(3’→5′)-N-[4-(dimethylethyl)benzoyl]-2′-O-(tetrahydromethoxypyranyl)cytidylyl-(3’→5′)-N-[4-(dimethylethyl)benzoyl]-2′-O-(tetrahydromethoxypyranyl)adenylyl-(3’→5′)-N-[4-(dimethylethyl)benzoyl]-2′-O-(tetrahydromethoxypyranyl)cytidylyl-(3’→5′)-N-[4-(dimethylethyl)benzoyl]-2′-O-(tetrahydromethoxypyranyl)cytidylyl-(3’→5′)-N-[4-(dimethylethyl)benzoyl]-2′,3′-O-(methoxymetylene)-octadecakis(2-chlorophenyl)ester. 5′-[2-(dibromomethyl)benzoate].
Самым длинным химическим названием обладает ДНК выделенное из митохондрии человека и состоящая из 16569 пар нуклеотидов. Полное название этого соединения содержит около 207 000 знаков.
Система из наибольшего числа несмешивающихся жидкостей, снова расслаивающаяся на компоненты после перемешивания содержит 5 жидкостей: минеральное масло, силиконовое масло, воду, бензиловый спирт и N-перфторэтилперфторпиридин.
Самая плотная органическая жидкость при комнатной температуре — это дииодметан. Его плотность составляет 3,3 г/см3.
Самыми тугоплавкими индивидуальными органическими веществами являются некоторые ароматические соединения. Из конденсированных это тетрабензгептацен (температура плавления +570 С), из неконденсированных — п-септифенил (температура плавления +545 С). Существуют органические соединения для которых не измерена точно температура плавления, например, для гексабензокоронена указывается, что его температура плавления выше 700 С. Продукт температурного сшивания полиакрилонитрила разлагается при температуре около 1000 С.
Органическое вещество, имеющее наибольшую температуру кипения — это гексатриаконилциклогексан. Он кипит при +551°С.
Самым длинным алканом, является нонаконтатриктан C390H782. Его специально синтезировали для исследования кристаллизации полиэтилена.
Самым длинным белком, является белок мышечной ткани титин. Длина его зависит от вида живого организма и локализации. Титин мыши, например, имеет 35213 аминокислотных остатков (мол. вес 3 906 488 Da), титин человека имеет длину до 33423 аминокислотных остатков (мол. вес 3 713 712 Da).
Самым длинным геномом, является геном растения Парис японская (Paris japonica). Он содержит 150 000 000 000 пар нуклеотидов — в 50 раз больше, чем у человека (3 200 000 000 пар нуклеотидов).
Самой большой молекулой, является ДНК первой хромосомы человека. Она содержит около 10 000 000 000 атомов.
Индивидуальным взрывчатым веществом с самой высокой скоростью детонации, является 4,4′-динитроазофуроксан. Его измеренная скорость детонации составила 9700 м/с. По непроверенным данным еще большей скоростью детонации обладает этилперхлорат.
Индивидуальным взрывчатым веществом с самой высокой теплотой взрыва, является этиленгликольдинитрат. Его теплота взрыва 6606 кДж/кг.
Самой сильн